0 引言

近年来，复杂网络引起了科学家的广泛关注^[1]。复杂网络最重要的统计特征是小世界效应^[2]和无标度特性^[3]，其中，小世界网络具有小的特征路径长度和大的簇系数，而无标度特性指的是网络的节点度(节点的度定义为与该节点相关联的边的条数)分布服从幂律^[4]。

复杂网络上的同步现象是一种重要的研究课题^[5-7]。研究表明，无标度网络和小世界网络的同步能力好于规则网络^[8]。对这一现象的普遍解释是小世界网络和无标度网络的平均最短距离小，使得信息之间的交流更高效。然而本文发现网络的同步能力几乎独立于网络的平均路径长度，即平均路径相同的网络同步能力却存在较大的差异。NISHIKAWA T、MOTTER A E等的研究表明，对无标度网络而言，网络度分布的不均匀性抑制了网络同步能力的增强^[9]；HONG H、KIM B J等的研究则表明，对WS小世界网络而言，使节点度分布变得不均匀(即增大度分布的方差)增强了小世界网络的同步能力^[10]，与文献的结论貌似冲突。本文对此给出了详尽的解释。

BARAHONA M和PECORA L M^[11]研究了线性耦合网络的同步稳定性问题，给出了主稳定函数判据。如果在网络的每个节点上放置一个动力学系统(该动力学系统既可以是极限环，也可以是混沌的)，让有边相连的两个节点的动力学系统之间存在相互耦合作用，就形成了一个动力学网络。设网络有N个节点,那么第i个节点所满足的状态方程是：

WS小世界网络的构造算法为：(1)给定一个节点数为N的规则网络，每个节点都与它最邻近的K=2k个节点相连，通常N≥K≥1；(2)依次访问网络中的每个节点，对每个节点的所有连线以概率p进行重连，连接该节点的一端不变，另一端随机选择节点连接，但两个节点之间不允许重复连接，也不允许节点与自身相连。

本文考虑了一种择优选择的小世界网络模型(Small-World Networks with Preferential Attachment，PA小世界网络)。其构造算法为：(1)步骤(1)与WS小世界网络模型相同；(2)在WS小世界网络断开重连时，不是随机选择一个节点连接，而是按照正比与节点度的概率选择节点连接。

1 网络几何特征量

1.1 簇系数

簇系数是表征网络节点集群程度的物理量。节点i的簇系数定义为所有相邻节点之间连边的数目与可能的最大连边数目的比例。假设节点i的度为k_i，它的所有邻居节点之间的边数为E_i，则节点i的簇系数定义为C_i=2E_i/(k_i(k_i-1))。对网络中所有节点的簇系数求平均值就是整个网络的簇系数。

1.2 特征路径长度

在网络中，两点间的距离定义为连接两点的最短路径所包含的边的数目，对所有节点对的距离求平均就得到了网络的特征路径长度。

1.3 节点度的方差

节点度的方差是衡量节点度分布均匀性的一种度量。度分布越均匀，方差越小；反之，方差越大。其定义为：

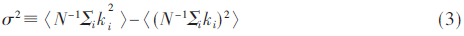
1.4 节点的介数

节点k的介数定义为：

式中，g_ij是节点i和节点j之间最短路径的条数，g_ikj表示节点i和节点j之间最短路径中经过节点k的条数。对网络中的所有节点对(i，j)求和即可以得到节点k的介数。由此可以看出，一个节点的介数反映了该节点在其他节点通信中的重要程度。

2 仿真结果

仿真中，选择网络节点数N=500(仿真表明，节点数的多少并不影响结果的普遍性)，K=2k=12，即网络的平均度=12。仿真图的数据为节点数N=500时程序运行50次的平均结果。

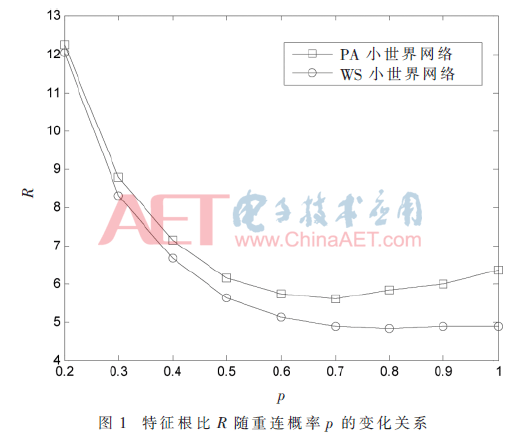
首先研究了特征根比例R随重连概率p的变化情况。如图1所示，对于PA小世界网络，随着的p增大，R值先是单调减小然后单调增大，表明该网络的同步能力随着p先增强后减弱；对于WS小世界网络，R单调递减，这表明WS小世界网络的同步能力随着p的增大而增强。那么发生这种差异的原因是什么呢？为此，本文还研究了网络的其他几何特征量，如网络的特征路径长度l和簇系数C(如图2所示)、节点度的方差σ²(如图3所示)、节点的最大介数B_max(如图4所示)以及节点的最大度数k_max(如图5所示)等随着p的变化情况。

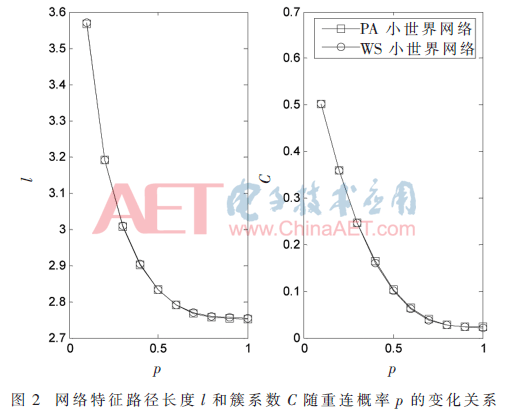
由图2可以看出，对于PA小世界网络和WS小世界网络，特征路径长度l和簇系数C都随着p的增加而单调减小，且几乎保持一致，这说明图1中R值的差异不是由特征路径长度l和簇系数C的不同引起的；同时，也表明对于特征路径长度和簇系数都几乎相同的网络，其同步性能仍然可以展现出相当的差异，也说明了两者中的任何一个都不是造成这种差异的原因。

图3是对PA小世界网络和WS小世界网络的节点度的方差仿真的结果。显而易见，PA小世界网络和WS小世界网络的节点度的方差都随着p的增大而增大，但在PA小世界网络中，由于重连时另一端为择优选择，导致节点度的方差增大的速度明显快于WS小世界网络。HONG H^[10]等人认为小世界网络中节点度的方差的增大会导致其同步能力的增强。本文的仿真也表明，在WS小世界网络中，随着p的增大，R逐渐减小，节点度方差σ²逐渐增大，那么是否节点度的方差的增大是导致网络同步能力增强的原因呢？答案是否定的。可以看到，在PA小世界网络中，随着重连概率p的增大，方差也逐渐增大，且增加的速率明显大于WS小世界网络，但由于节点度的方差增加的太快，使得这种度分布的不均匀性对网络的同步能力起了抑制作用(如在图1中当p≥0.7时R值的上扬，表明了PA小世界网络同步能力的下降)。从图1可以看出，在整个p值的范围内，PA小世界网络的同步能力明显不及WS小世界网络(因为R_PA>R_WS)。

另由图3可知，在整个p值的范围内，PA小世界网络的节点度的方差始终大于WS小世界网络。因为两种网络的网络特征路径长度l和簇系数C几乎相等(由图2可知)，由此可以推断，节点度的不均匀性实际上对网络的同步能力起抑制作用。由此，在WS小世界网络中，增强网络同步能力的主要因素不是节点度方差逐渐增大(节点度方差只是由于小世界网络中边的重连引起的一种很自然且必然的结果)，网络的特征路径长度下降才是最主要的原因(当p值较小时，尽管度分布的不均匀性抑制了网络的同步能力，但由于网络的特征路径长度大幅下降，网络的同步能力还是增强了；但是，当网络的特征路径长度下降几乎为常数时，如果节点度分布的方差大于一定的临界值，其抑制作用就比较明显了，如图1和图3所示)。所以，短的特征路径长度和均匀的节点度分布综合作用才能导致网络同步能力的增强。此外，NISHIKAWA T^[9]和HONG H^[10]均认为网络节点的最大介数B_max是表征网络同步能力的一种相对合理的因素。降低网络节点的最大介数B_max将导致网络同步能力的增强。图4的仿真结果也说明了这个问题。可以看到，在PA小世界网络中，B_max随p先是单调下降然后单调上升，与R随p的变化趋势相同。所以，网络中节点的最大介数B_max的确可以作为表征网络同步能力的一种度量。

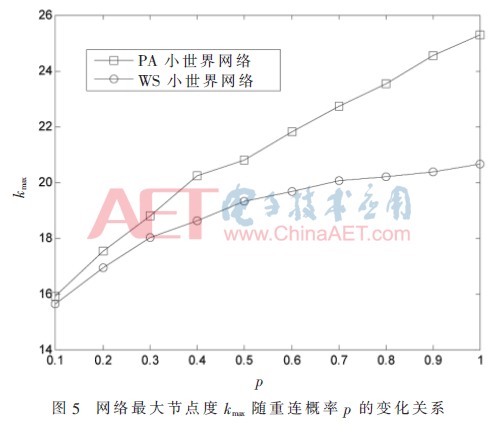
由图4可知，在整个p值范围内，PA小世界网络中节点的最大介数始终大于WS小世界网络中节点的最大介数；而图1中，在整个p值范围内，PA小世界网络的同步能力始终不及WS小世界网络，这从另外一个侧面反映了最大介数表征网络同步能力的合理性。在无标度网络中，网络中最大节点度k_max和最大介数B_max是正相关的，即k_max越大，通常B_max也越大；在WS小世界网络中，变化呈相反的趋势，随着k_max的增大，B_max单调下降，如图4和图5所示，在PA小世界网络中，k_max和B_max呈现一种相对微妙复杂的关系。

3 结论

本文研究了一种择优选择的小世界网络模型，基于这种模型，详尽地研究了网络的同步能力与网络中的各种几何特征量(如网络平均路径、簇系数、度分布以及介数等)之间的关系。研究结果表明，网络的特征路径长度和簇系数都不能单独决定网络的同步能力，因为，在两者都相等的情况下网络仍然可以有很多不同的配置，因而网络的同步能力仍然可以存在较大的差异。节点度分布的不均匀性从本质上抑制了网络的同步能力。仿真结果表明，网络中节点的最大介数是表征网络同步能力的一种相对统一的物理量。

参考文献

[1] NEWMAN M E J.The structure and function of complex networks[J].SIAM Review，2003，45(2)：167-256.

[2] WANG X F，CHEN G R.Synchronization in small-world dynamical networks[J].Bifurcation and Chaos，2002，12(1)：187-192.

[3] LI Z，CHEN G R.Global synchronization and asymptotic stability of complex dynamical networks[J].IEEE Transactions Circuit and System，2006，53(1)：28-33.

[4] WANG X F, CHEN G R.Synchronization in scale-free dynamical networks：robustness and fragility[J].IEEE Transactions on Circuits and Systems I，2002，49(8)：54-62.

[5] ZHAO M，ZHOU T，WANG B H，et al.Relations between average distance, heterogeneity and network synchronizaility[J].Physica A，2006，371(2)：773-780.

[6] WU X，WANG B H，ZHOU T，et al.Synchronizability of highly clustered scale-free networks[J].Chinese Physics Letters，2006，23(4)：1046.

[7] 魏民，王莉，张强.基于复杂网络理论的典型电力电子电路复杂性研究[J].电子技术应用，2011，37(9)：118-121.

[8] MOTTER A E，ZHOU C，KURTHS J.Network synchronization，diffusion，and the paradox of heterogeneity[J].Physical Review E，2005，71(1)：016116.

[9] NISHIKAWA T，MOTTER A E，LAI Y C，et al.Heterogeneity in oscillator networks: are smaller worlds easier to synchronize?[J].Physical Review Letters，2003，91(7)：014010(1-4).

[10] HONG H，KIM B J，CHOI M Y，et al.Factors that predict better synchronizability on complex networks[J].Physical Review E，2004，69(6)：067105(1-4).

[11] BARAHONA M，PECORA L M.Synchronization in small-world systems[J].Physical Review Letters，2002，89(5)：054101(1-4).

作者信息：

吕 瑛，李颖华

(西北工业大学明德学院 信息工程学院，陕西 西安710124)