0 引言

传统A/D采用香农-奈奎斯特采样理论，采样速率至少等于信号带宽的两倍才能无失真地恢复。香农-奈奎斯特采样理论是可以重构信号的充分条件，而不是必要条件。理论上存在另外一种低于奈奎斯特速率的采样方法，通过这种方法也可以重构恢复原信号。压缩感知(Compressed Sensing，CS)^[1-2]就是这样一种革命性的采样转换技术，如果信号可以稀疏表示^[3-4]，压缩感知能够从少于香农-奈奎斯特采样的样值中恢复信号。无线通信中的信号大多可以稀疏表示，例如超宽带信号在时域中可以稀疏表示^[5-6]，跳频信号在频域可以稀疏表示^[7]。

压缩感知用于重构可稀疏表示的信号，使其不失真地以奈奎斯特速率表示。一些应用有时候只关心传输信号中的信息，而不需要重构原信号。压缩信号处理是一种直接处理压缩后信号的方法，它只是关心信号中的有用信息而不是重构^[8]。区别于压缩信号的恢复，本文对信号传输信道的估计和信号的检测更感兴趣，文中主要解决二进制偏移载波调制信号检测问题。压缩感知已经应用到扩频系统中伪随机序列的捕获^[9-10]，相关峰值在码相位和频偏组成的二维空间中是稀疏的。CS可以用于降低GPS接收机的采样频率^[11]，但是其硬件实现较为复杂。文献[12]指出的扩频接收机利用压缩感知简化接收机设计，该文中对几种接收机进行了对比，并分析了量化的影响。应用压缩信号处理对直接序列扩频信号欠采样解调^[13]，可以降低功耗和接收机的制造成本，而且采用匹配滤波器比随机解调器更为简单。文献[14]在频率选择信道上，构建直接序列扩频通信系统的信道估计和符号检测模型，并分析了基于不同算法下的误码率性能，表明采用CS辅助的SLSS-JCESD接收算法降低一半采样速率，会损失1.2 dB的SNR。

现代GPS、Galileo、北斗等导航卫星系统中，都启用了二进制偏移载波(Binary Offset Carrier，BOC)调制技术。与传统的BPSK相比，BOC调制在载波调制之前增加了一个副载波调制环节。副载波是基于正弦相位或者余弦相位的方波，这两种分别记为BOC_sin(Kn，n)和BOC_cos(Kn，n)，其中K表示副载波频率与伪码速率的比值，n表示伪码速率与f₀=1.023 MHz的比值。与BPSK信号频谱分布在载波处不同，BOC信号的频谱主瓣分布在载频±Knf₀处，这使得BOC信号具有更宽的频谱，其带宽通常记为副载波频率与伪码码率之和的两倍。针对BOC调制信号的特征，本文中提出一种基于压缩感知的BOC信号接收机和发射机模型，并且采用压缩信号处理的方式对接收到的BOC信号解调。收发机模型中匹配滤波器的使用，降低了扩频通信系统的实现复杂度。并且通过大量的仿真实验，对压缩接收机和传统接收的误码性能进行分析对比。

1 信号模型

一个通用测量系统可以通过式(1)进行描述：

其中，x是N×1维被测量向量，Φ表示M×N维的测量矩阵，M×1维向量y是测量值。测量矩阵中每个行向量对x的观测值，组成测量值向量y中的元素。测量可以简单地描述为通过测量值y和测量矩阵Φ，求得未知值x。

目前，传统采样技术基于香农-奈奎斯特采样理论。对于香农-奈奎斯特测量系统，式(1)中，M=N，并且?椎是N×N维的单位矩阵。香农-奈奎斯特采样理论揭示了这种测量系统可以无失真恢复被测量值的条件。

式(1)中当M>N时，即得到的测量值数量多于未知被测量个数，与M=N类似，可以唯一地求解出被测量值。

下面考虑式(1)中M

1.1 发射机模型

带通信号可以用其低通等效进行表示，即可以用处理低通等效信号代替处理带通信号，这样就减少了对信号进行分析和仿真的复杂度。BOC基带信号的生成可以分离为两部分：基于BPSK基带信号的扩频调制、基于余弦或正弦相位的方波副载波调制，如图1所示。

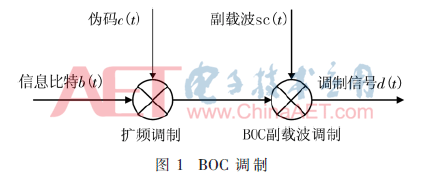
在发射机和接收机中，假设一次处理一个符号，该符号中包含一个或多个信息比特，即向量b∈{±1}^L×1是传输的一个符号，每个符号由L比特数据组成。定义伪随机序列向量为c∈{±1}^C×1，其中包含C个码片。上述两个向量是图1中b(t)和c(t)离散表达。如果定义T_b和T_c分别表示数据信息周期和码宽，则有LT_b=CT_c，即一个符号周期中含有整数个伪码周期。BOC_sin(Kn，n)基带信号中的一个符号可以通过式(2)表示：

其中，Ψ是由伪随机序列组成的字典，它的每一列都是一个可能传输的扩频调制信号；a∈{0，1}^M×1是稀疏向量，仅有一个值不等于零，用于选择从字典中选择要发送的伪随机序列。向量a的稀疏度决定了可以采用压缩感知的方法对BOC信号进行解调。

1.2 BOC压缩信号处理接收机原理

信号在传输的过程中会受到噪声的干扰，接收机接收到的信号通常可以描述为:

其中，n(t)是加性高斯白噪声。接收信号的匹配滤波接收机结构如图2所示^[17]，接收信号先进行匹配滤波，然后以伪码速率进行采样，最后进行解扩。

假设信号在接收机端已经完全同步，接收信号中一个符号的接收采样过程可以通过式(6)表示：

基于硬件压缩采样结构的随机解调器中，接收信号首先需要与伪随机序列相乘，然后通过低通滤波^[4]。BOC信号在发射端已经通过伪随机序列进行频谱扩展，因而在接收端伪随机码产生器可以省略。BOC信号的调制过程中，使用副载波波形作为脉冲成型波形，因此采样之前的匹配滤波器需要做相应的修改。基于硬件压缩采样的BOC信号接收欠采样过程为：

其中，θ_i(t)=sc(t-iT_c)，0≤tc，是匹配滤波器。κ=I/L∈(0，1]是压缩感知结构中的欠采样因子，当κ=1时没有进行压缩，κ越小得到的采样值数量相对于奈奎斯特采样值的个数越少。Θ=[θ₀(t) θ₁(t) … θ_C-1(t)]^T是测量矩阵，经过测量采样每比特信息得到I=Cκ个样值。

在接收端，本文的目的是解调出a，因而不需要重构出压缩感知的原始信号b(t)。可以通过压缩信号处理的方法^[8]，在压缩域直接对压缩信号进行处理解调出信息比特。通过压缩信号处理的方法对信号解调减小计算复杂度，省去了信号重构的过程。

2 仿真实验

为了描述基于压缩信号处理的接收机性能，分别采用奈奎斯特采样和压缩感知硬件采样对BOC信号接收解调，并比较在高斯白噪声信道下各自的误码率性能。文中仅在理想的情况下对BOC解调算法进行分析，不考虑载波频偏的影响，并且认为信号已经同步。实际应用中，载波的剥离可以通过载波跟踪算法完成，码字的同步亦可由延迟锁定环确定。

为方便且不失一般性，仿真中采用BOC（1，1）信号，伪随机码周期中含有32个码片，每比特信息用一个周期的32码片进行扩频。仿真采用蒙特卡罗算法，设置错误信息比特门限为100，在相同的Eb/N0的情况下对比两种解调方法的误码率。仿真结果如图3所示，在压缩率κ=0.5的情况下，为得到同样的误码性能(误码率10^-5)，使用压缩信号处理解调BOC信号比采用经典方法解调BOC信号需要高出3 dB左右的信噪比。但是采样速率降低了1/2，后续处理的计算量减少了一半。压缩信号处理方法中，解调损失的信噪比是由噪声折叠引入^[18]。

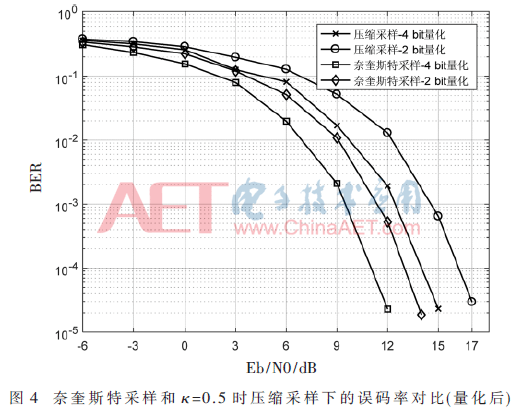
采样后需要量化，量化分辨率影响误码性能，如图4所示。为了评定压缩采样和奈奎斯特采样量化后对误码性能的影响，在相同的量化总比特数下对其进行对比。也就是说，奈奎斯特采样速率下2 bit量化和1/2压缩采样下4 bit量化具有相同的量化总比特数。对比这两种情况，同样达到误码率10^-5，压缩采样所需的信噪比仅仅比奈奎斯特采样多1 dB。在采样率受限的情况下，可以通过增加量化分辨率改善误比特性能。

3 结论

本文应用压缩感知的方法产生BOC信号，副载波波形为其成型波形，并采用压缩信号处理对BOC信号解调。解调算法不同于随机解调器，接收端不需要与随机序列相乘，实现简单。这种基于压缩信号处理的BOC信号解调方案所需要的采样速率低于奈奎斯特采样速率，有利于降低系统功耗和器件成本。压缩信号处理可以解决目前信号处理的瓶颈，即越来越高的采样频率、大量数据的存储处理和分析。可以想象压缩信号处理有着广泛的应用空间，特别是对高带宽的扩频信号，压缩信号处理有天然的吸引力。

参考文献

[1] CANDES E J，ROMBERG J，TAO T.Stable signal recovery from incomplete and inaccurate measurements[J].Communications on Pure and Applied Mathematics，2006，59(8)：1207-1306.

[2] DONOHO D L.Compressed sensing[J].IEEE Transaction on Information Theory，2006，52(4)：1289-1306.

[3] TROPP J A，LASKA J N，DUARTE M T，et al.Beyond Nyquist：efficient sampling of sparse bandlimited signals[J].IEEE Transaction on Information Theory，2010，56(1)：520-544.

[4] 翁天阳，庄宇，于玮，等.基于HPS和FPGA的图像压缩感知编解码系统[J].电子技术应用，2017，43(5)：90-93.

[5] OKA A，LAMPE L.A compressed sensing receiver for UWB impulse radio in bursty applications like wireless sensor network[J].Physical Communication，2009，2(4)：248-264.

[6] PAREDES J L，ARCE G R，WANG Z.Ultra-wideband compressed sensing：channel estimation[J].IEEE Journal of Selected Topics in Signal Processing，2007，1(3)：383-395.

[7] LASKA J，KIROLOS S，MASSOUD Y，et al.Random sampling for analog-to-information conversion of wideband signals[C].IEEE DCAS Workshop，Dallas，TX，USA，2006：119-122.

[8] DAVENPORT M A，BOUFOUNOS P T，WAKIN M B，et al.Signal processing with compressive measurements[J].IEEE Journal of Selected Topics in Signal Processing，2010，4(2)：445-460.

[9] AGGARWAL V.Enhanced CDMA communications using compressed-sensing reconstruction methods[C].47th Annual Allerton Conference on Communication，Control，and Computing，Illinois：UIUC，2009：1211-1215.

[10] 郑昆，张晓林.一种改进的BOC(kn，n)信号无模糊跟踪方法[J].电子技术应用，2018，44(9)：116-120.

[11] LI X.GPS signal acquisition via compressive multichannel sampling[J].Physical Communication，2012，5(2)：173-184.

[12] FYHN K，JENSEN T L，LARSEN T，et al.Compressive sensing for spread spectrum receivers[J].IEEE Transactions on Wireless Communications，2013，12(5)：2334-2343.

[13] FYHN K.Demodulating subsampled direct sequence spread spectrum signals suing compressive signal processing[C].20th European Signal Processing Conference，Bucharest，Romania：EUSIPCO，2012：2556-2560.

[14] Wang Shuai，An Jiangping，Ren Yanyang，et al.Compressed receiver for multipath DSSS signals[J].IEEE Communcations Letters，2014，18(8)：1359-1362.

[15] BETZ J.Binary offset carrier modulation for radionavigation[J].Navigation：Journal of the Institute of Navigation，2001-2002，48(4)：227-246.

[16] PRATT A，OWEN J.BOC modulation waveforms[C].ION GPS/GNSS，Portland，OR：ION，2003：1044-1057.

[17] PROAKIS J G，SALEHI M.Digital communications(5th Edition)[M].New York：McGraw-Hill，2008.

[18] METZLER C A，MALEKI A，BARANIUK R G.From denoising to compressed sensing[J].IEEE Transactions on Information Theory，2016，62(9)：5117-5144.

作者信息:

宋 朋1，何国栋2

(1.中国电子科技集团公司第五十八研究所，江苏 南京210000；

2.安徽师范大学 物理与电子信息学院，安徽 芜湖241003)