文献标识码: A
DOI:10.16157/j.issn.0258-7998.190146
中文引用格式: 姚荣欢. 基于小波神经网络的数据中心KPI预测[J].电子技术应用,2019,45(6):46-49,53.
英文引用格式: Yao Ronghuan. Data center KPI prediction based on wavelet neural network[J]. Application of Electronic Technique,2019,45(6):46-49,53.
0 引言
随着软件和微服务的发展,智能运维越来越受到人们的重视。在大量的运维数据里,最不可忽视的就是各种关键性能指标数据(Key Performance Indicators,KPI),它们在数学上都可以被表达为时间序列的形式。在一个大型软件系统里,往往每分钟能产生百万数量级的时间序列,如何从这些海量数据里发现规律,指导运维并将其智能化,成为了下一代运维中最重要的环节之一。智能运维的一个主要挑战是根据具体需求评判应用哪些机器学习算法,并适配或改造。智能数据中心关键性能指标数据异常检测是智能运维的重要环节,可以作为运维人员的可靠助手,从而大大减少人力投入并增加运维安全性。而时间序列预测是时间序列异常检测的重要组成部分。本文利用小波神经网络对时间序列进行预测,并采用动量梯度下降算法和粒子群优化算法对小波神经网络进行了优化,在一定程度上提高了时间序列预测的准确性。
1 KPI概述
1.1 时间序列特点
(1)长期趋势(Trend):现象在较长时期内受某种根本性因素作用而形成的总的变动趋势;
(2)循环变动\周期性(Cyclic):现象以若干年为周期所呈现出的波浪起伏形态的有规律的变动;
(3)季节性变化(Seasonal variation):现象随着季节的变化而发生的有规律的周期性变动;
(4)不规则变化(Irregular movement):是一种无规律可循的变动,包括严格的随机变动和不规则的突发性影响很大的变动两种类型[1]。
1.2 KPI特点
KPI是一种特殊的时序数据,与普通时序数据相比,存在更多的形状变化。常见的形状变化主要包括以下几种:
(1)噪声和异常:曲线上与正常值不符的波动。
(2)振幅差异:KPI曲线可能具有不同量级的振幅,例如同一服务的两个相关但不同模块的每秒查询率曲线。
(3)相位偏差:两条KPI曲线之间的整体相位偏移。例如,同一系统调用链上的一组KPI可能具有相似的形状,但存在一定的时延,从而产生相位偏差。
2 小波神经网络
2.1 小波神经网络原理
小波变换针对傅里叶变换的不足发展而来。傅里叶变换把信号按三角正、余弦基展开,能较好地刻画信号的频率特性,但在时域或空域上却无任何分辨,不能做局部分析。而小波变换有一个灵活可变的时间-频率窗,在时域和频域同时具有良好的局部化特性。
小波神经网络是基于小波变换以及小波构造理论所搭建的多分辨率、多层的神经网络,即用小波基来取代常用的Logistic传递函数[2]。
2.2 小波神经网络的优点
(1)小波变换通过平移和伸缩变换对信号进行多尺度分析,能有效提取信号的多尺度信息;
(2)神经网络具有容错性、自学习、自适应等特点,是一类通用的函数逼近器;
(3)小波神经网络的基元和整个结构由小波分析理论确定,可避免BP神经网络等在结构设计上的盲目性;
(4)小波神经网络精度更高,学习性更强;
(5)小波神经网络结构简单,收敛速度更快。
2.3 小波神经网络类型
(1)松散型:小波分析对神经网络的输入进行初步处理,使得输入信号更利于神经网络处理;
(2)融合型:神经网络与小波直接融合,用小波元代替神经元,输入层到隐含层的权值及隐含层阈值分别由小波函数的尺度和平移参数确定[3-4]。
2.4 拓扑结构
本文构造的三层小波神经网络拓扑结构如图1所示。图中,X为输入,Y为输出,Ψa,b(t)为隐藏层。
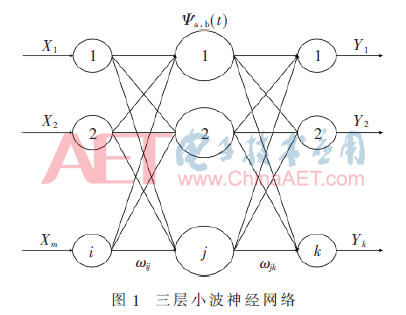
2.5 神经元节点数确定
小波神经网络输入层神经元个数由输入数据特征向量的维数决定,输出层神经元个数由网络预测值个数决定。隐藏层节点数没有具体确定的计算方法。隐藏层节点数太少则可能出现欠拟合,隐藏层节点个数太多则容易过拟合,并且训练时间增加。假设输入层有L个节点,输出层有N个节点。则隐藏层节点个数选择可参考公式有:

式中,M为隐藏层节点个数,a为0~10之间的常数。
实际应用时可根据参考公式确定隐藏节点数的大概范围,然后使用误差率调整节点个数。本文选择式(2)。
2.6 传递函数
2.6.1 隐藏层传递函数
本文构造的神经网络隐含层采用的小波基函数为Morlet母小波基函数,数学公式为:

函数图形如图2所示。
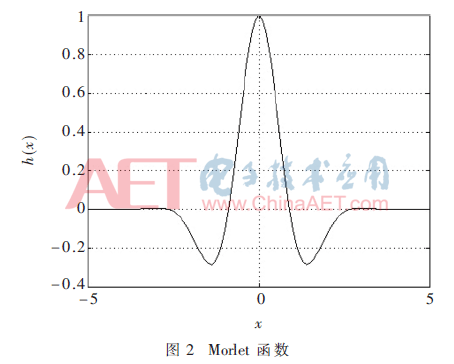
因此隐含层输出计算公式为:

式中,hj为隐含层第j个节点输出值,wij为输入层到隐含层的连接权值,bj为小波基函数的时移因子,aj为小波基函数的频率因子。
2.6.2 输出层传输函数
本文构造的神经网络输出层采用线性函数,数学公式为:

函数图形如图3所示。
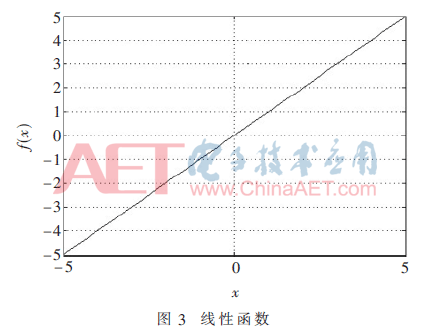
因此输出层计算公式为:

式中,Ok为输出层第k个节点输出值,wjk为隐含层到输出层的连接权值,hj为隐藏层输出[5-7]。
2.7 附加动量梯度修正法
梯度学习优化算法因其学习速率的不变性致使神经网络收敛速率很慢并且容易陷入局部最优,可以通过附加动量法提高网络学习效率。

即k+1次迭代动量项为上k次和k-1次参数取值之差。
3 粒子群算法优化小波神经网络
3.1 粒子群算法简介
粒子群(PSO)算法从鸟类种群捕食行为特征得到启发,算法每个粒子代表一个潜在解,粒子速度代表了粒子移动方向和距离,速度根据自身及其他粒子的经验动态调整。
具有D个参数的优化问题构成D维搜索空间,初始化N个粒子组成种群X=(X1,X2,…,XN),第i个粒子Xi=(xi1,xi2,…,xiD)。根据优化目标计算粒子适应度,第i个粒子的速度Vi=(vi1,vi2,…,viD),每次迭代记录个体极值Pi=(pi1,pi2,…,piD)(从开始迭代到本次迭代个体粒子使用度最佳位置),以及种群群体极值Pg=(pg1,pg2,…,pgD)。粒子根据个体极值和群体极值的启发式信息更新位置,公式如下:
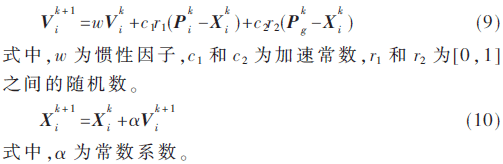
3.2 粒子群算法优化过程
3.2.1 基本思想
基于粒子群优化算法优化小波神经网络的基本思想:将各连接权值和小波伸缩以及时移参数作为粒子群算法的微粒向量,每一个微粒向量经过解码到各个系数。网络将训练样本输入,计算输出和误差,将误差的倒数作为适应度函数(误差越小,适应度越大)。然后将粒子群算法的最优值赋给小波神经网络以代替小波神经网络初始随机赋值,最后小波神经网络根据反向传播算法训练直至收敛[8-9]。
3.2.2 算法步骤及流程
算法主要分为3个阶段:
(1)构建小波神经网络;
(2)使用粒子群算法训练网络;
(3)将粒子群算法训练得到的最优解作为网络参数初始值,使用反向传播算法训练网络。
算法流程如图4所示。

3.2.3 粒子解码
假设网络的拓扑结构为输入层L个节点,隐藏层M个节点,输出层N个节点。则网络输入层到隐藏层L×M个权值参数,隐藏层到输出层有M×N个权值,隐藏层每个节点还有一个时移参数和一个频率参数共2×N个参数,因此共L×M+2×N+M×N个参数。粒子向量编码顺序为前L×M个参数为输入层到隐藏层L×M个权值,然后N个参数为频率参数,其次N个参数为时移参数,其余参数为隐藏层到输出层的M×N个权值[10-13]。
4 实验结果与分析
4.1 实验环境
本实验操作系统为Linux-3.13.0-57-generic-x86_64-with-Ubuntu-14.04-trusty,开发语言为MATLAB 7.9.0(R2009b),在Vim开发环境下进行。
4.2 数据集描述
为验证本文算法的有效性,选取某数据中心KPI指标1 210个。其中,905个作为小波神经网络训练数据,305个作为预测数据。数据集部分示例如表1所示。

4.3 评价准则
针对预测结果,本文采用两种度量标准:
(1)平均绝对误差,公式如下:
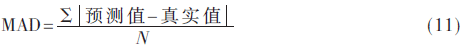
(2)皮尔森相关系数,公式如下:

4.4 实验结果
小波神经网络预测实验结果如图5、图6所示。
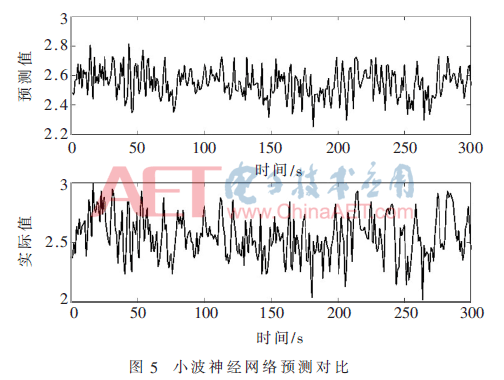
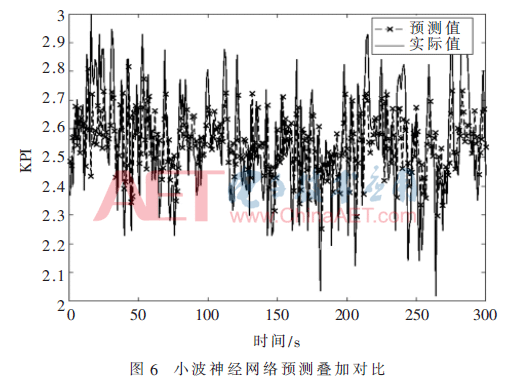
由图5、图6可以看出小波神经网络预测结果与原KPI序列相似程度较高,具体数值与趋势性预测均较为准确。
本文利用传统Arima(Autoregressive Integrated Moving Average Model)算法进行了对比试验[14],实验结果如图7、图8所示。
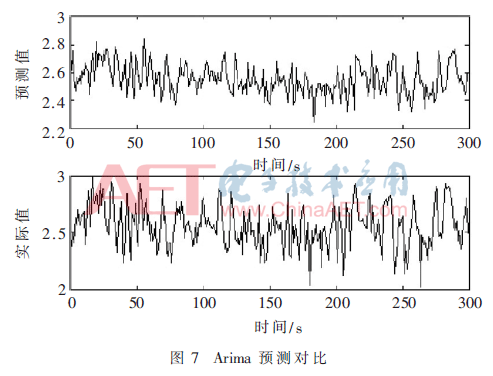
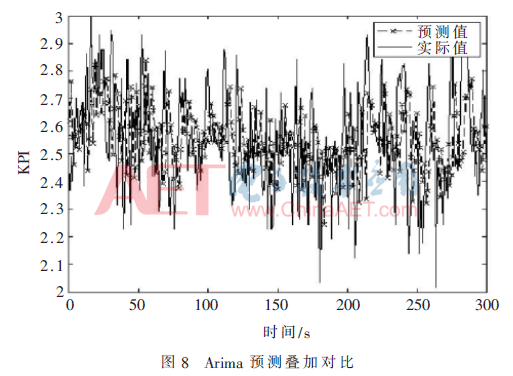
由图7、图8可以看出传统Arima模型也能较好地预测KPI数值及趋势,具体性能对比由表2所示。
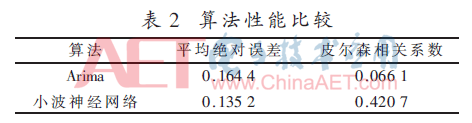
由表2可以看出,小波神经网络与传统Arima算法在平均绝对误差上表现出一定优势,说明小波神经网络预测值更加贴近原序列真实值。而在皮尔森相关系数的表现上,小波神经网络呈现出极大的优势,说明小波神经网络预测结果与原时间序列相关性更高,更加可信。
5 结论
本文提出利用粒子群算法优化小波神经网络并用附加动量梯度修正法加速小波神经网络学习速率来解决智能数据中心KPI预测的方法。该方法能以较高准确率和相关性对KPI时间序列进行预测,在与传统Arima算法的对比中显示了较为明显的优势。这将为数据中心KPI异常检测提供算法技术支持。
参考文献
[1] 张玲,刘波.基于残差统计的时间序列加性离群点检测算法研究[J].电子技术应用,2015,41(9):85-87.
[2] 刘建成,蔡湛宇.基于神经网络的脑电信号的非线性预测[J].电子技术应用,1999(7):14-15.
[3] 李静雯,杨善红.基于灰色Verhulst-小波神经网络的装备故障预测研究[J].电子技术应用,2014,40(8):91-93.
[4] 李银国,张帮礼.小波神经网络及其结构设计方法[J].模式识别与人工智能,1997(3):197-205.
[5] 臧川,江冰,薛心怡,等.基于小波优化神经网络的故障定位算法研究[J].电子技术应用,2014,40(6):55-58.
[6] 吴祖堂.基于神经网络预测器的传感器数据证实技术研究[J].电子技术应用,2001,27(1):22-25.
[7] 刘毅睿,谢芊,吕述望.白噪声序列检验的小波分析方法[J].电子技术应用,2005,31(10):48-49.
[8] 鲁旭阳,刘广怡,张效义.基于改进粒子群优化的节点定位算法[J].电子技术应用,2012,38(11):112-115.
[9] 李世文,张红梅,张向利,等.基于二进制粒子群与遗传算法的数据分配研究[J].电子技术应用,2016,42(7):122-125.
[10] 张朝龙,江巨浪,江善和,等.基于改进PSO算法的LSSVM入侵检测模型[J].电子技术应用,2010(10):132-135.
[11] 陈双叶,徐文政,丁双春,等.改进PSO-TSFNN智能家居室内空气质量检测与评价[J].电子技术应用,2017(1):84-87,91.
[12] 郝杰.基于改进小波神经网络的上证指数预测研究[D].广州:华南理工大学,2014.
[13] 赵学智,邹春华,陈统坚,等.小波神经网络的参数初始化研究[J].华南理工大学学报(自然科学版),2003,31(2):77-79,84.
[14] 涂小萌,陈强国.基于ARIMA-LSSVM混合模型的犯罪时间序列预测[J].电子技术应用,2015,41(2):160-162.
作者信息:
姚荣欢1,2
(1.华北计算机系统工程研究所,北京100083;2.中软信息系统工程有限公司,北京100081)

