0 引言

在频谱资源日益缺乏的情况下，提高频谱利用率增加用户连接数成为5G无线网络的一个研究方向^[1]。非正交多址接入(Non-Orthogonal Multiple access，NOMA)突破了传统的正交限制，其核心思想是通过码域或功率域的多路复用使更多的用户使用相同的时频资源传输信息，从而实现过载，提高频谱利用率^[2]。多天线技术因能充分利用空间资源而受到广泛的研究。NOMA与多天线技术的结合可以进一步提高系统的性能，目前引起了一些研究者的热切关注^[3]。

在上行免调度NOMA系统中不需要动态调度,减少了传输时延，节约了信令开销^[4]。但是基站无法获得用户的活动信息，因此，需要对用户的活动进行检测。有关统计表明：当前的通信系统中，进行通信的用户数量远远小于系统中总用户的数量^[5]，即用户的活动是稀疏的，这一特点在海量的连接的5G通信系统中依然存在。这样，多用户的检测问题就转化成稀疏信号的恢复问题，激发了研究者利用压缩感知(Compressed Sensing，CS)算法来实现多用户检测^[6]。文献[7]通过考虑用户活动在相邻时隙之间的联系，提出一种基于动态压缩感知（Dynamic Compressive Sensing，DCS）的多用户检测算法。文献[8]提出一种基于压缩感知的消息传递算法（Compressive Sensing based Message Passing Algorithm，CS-MPA）,这些算法需要已知活跃用户的数量，在实际的通信中并不适用。通过利用用户活动的结构稀疏性，文献[4]和文献[1]分别提出了结构化迭代支撑检测算法(Structured Iterative Support Detection，SISD)和联合近似消息传递(Approximate Message Passing，AMP)以及期望最大化(Expectation Maximization，EM)算法，在稀疏度未知情况下实现了免调度上行NOMA系统中用户活动和数据的联合检测，但复杂度较高。

受上述文献启发，本文考虑了基站端配备多根天线的情况。通过与传统的稀疏度自适应匹配追踪(Sparsity Adaptive Matching Pursuit，SAMP)算法结合，提出一种基于SAMP的硬融合算法(Hard Fusion Algorithm，HFA)。该算法能够在稀疏度未知的情况下对用户的活动及数据进行检测。在接收端的每根天线上只需用SAMP算法估计用户活动信息，通过对多根天线的检测结果进行融合进而提高活跃用户信息检测的准确性。

1 系统模型

考虑一个上行SIMO-NOMA系统，其中有一个基站和K个用户，基站端有N_B根天线，每个用户都有一根天线。活跃用户k的传输符号x_k为调制后符号，非活跃用户的传输符号为0。首先对符号x_k进行扩频，扩频序列s_k的长度为N，且N

2 检测算法SAMP-HFA

文献[5]指出，同一时隙内，活跃用户数一般不超过总用户数10%，即用户的活动情况是稀疏的。文献[4]将一个稀疏度为s信号的支撑集定义为：

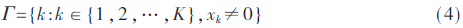
该集合表示x中非零元素的位置，检测用户活动信息的过程即求解该集合的过程。

在压缩感知理论中，如果观测矩阵A^l满足限制等容条件（Restricted Isometry Property，RIP），就可以将稀疏信号x高概率重构。这里，如果存在一个常数δ∈(0，1)使得对于任何一个稀疏度为s的信号满足式(5)，那么矩阵A^l就满足s阶RIP。已有研究表明高斯随机矩阵是普适的压缩感知测量矩阵，基于伪随机噪声序列的托普利兹矩阵可以高概率满足RIP^[9]，因此，在该系统中可以使用压缩感知的方法进行用户检测。

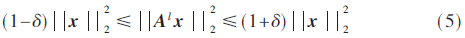
2.1 SAMP算法不足

在压缩感知检测算法中，SAMP算法^[10]是经典的适用于稀疏度自适应的一个，但是它存在两点不足：

(1)在有噪的非正交多址接入系统中该算法不适用。文献[10]指出当测量值y^l为无噪信号时，其迭代停止阈值为ε=0；当y^l为有噪信号时，ε为噪声的能量，即ε=norm(v^l)，但是在实际中噪声并不可知，因此无法获取迭代停止阈值。

(2)无法准确估计信号稀疏度。在设定迭代步长时，设定得过小会使运算时间大大增加，但是过大又会出现过匹配或欠匹配的情况，影响检测的准确性。

2.2 SAMP-HPA算法流程

本文所提算法主要是从以上两点出发：首先是如何获取SAMP算法的停止阈值，其次是如何改善该算法中原子过匹配或欠匹配问题。其流程主要包括以下三部分：

第一部分设定阈值时，首先需要根据系统的信噪比估计阈值的大小。当设定阈值小于估计阈值时，在每根天线使用SAMP算法检测出来的活跃用户比实际的多，这个活跃用户的集合中包含大多数甚至是全部的活跃用户。针对不同的情况，设定阈值时需遵循以下两点：①信噪比较小时，噪声干扰较大，检测出的活跃用户的准确性较低，为提高融合后活跃用户信息的准确性，在每根天线需要检测出较多的用户参与第二部分的融合，因此应适当增大设定阈值与估计阈值的差值；随着信噪比的增大，各天线检测出的活跃用户集合相对准确，此时应适当减小设定阈值与估计阈值的差值。②当天线的数目较少时，只需综合少数天线的检测信息，漏检概率较小，应减小设定阈值与估计阈值的差值；随着天线数目的增加，参与融合的天线越来越多，融合过程中综合的天线检测信息增加，漏检概率相对也会增加，因此应增大设定阈值与估计阈值的差值，使每根天线检测出更多的用户参与融合。

第二部分融合每根天线上用户活动信息时结合了m秩准则。在本文意为：当N_B根天线中有m根天线检测出某用户是活跃的就认为该用户是活跃的。它是OR准则和AND准则的折中。当m=N_B时，该准则等同于AND准则，当m=1时等同于OR准则^[12]。该准则能够提高融合后活跃用户信息正确性，进而使得系统的检测性能提高。当天线数目N_B=2时，m的取值为2，即为AND准则，当天线的数目增多时，通过选择合适的值来融合多根天线上的用户活动信息。

针对某用户，使用m秩准则进行融合的全局检测概率P_D和虚警概率P_F可表示如下：

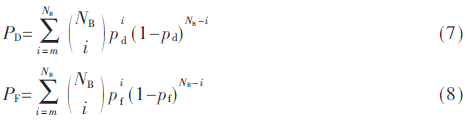
其中，p_d和p_f分别表示每根天线对某一用户的检测概率和虚警概率，对于OR准则，其全局漏检概率最低，但是虚警概率最高，AND准则与之相反。而m秩准则可以有效避免上述两种准则所产生的极端后果，通过选择合适的m值对每根天线上的检测结果进行融合，提高融合后活跃用户集合的准确性，进而提高整个系统的检测性能。

在对用户的活动信息进行融合时，可使用如下方法进行处理。基本思想是根据每个用户被基站端的多根天线检测出来的频率来判断它是否活跃。本文用w^l表示第l根天线上的判决向量，若第l根天线检测用户k活跃，则w^l，k=1，否则w^l，k=0，根据每根天线检测的活跃用户集合，将w^l的相应位置设置为1。因此，在每根天线都可以得到一个包含用户活动信息的判决向量，并且将所有判决向量对应相加便可以得到最终的判决向量w，结合m秩准则，根据此向量各位置的数值判断用户是否活跃，即当w中的元素值大于等于m时，就认为这些用户是活跃的，最终可以得到一个融合后的公共的活跃用户的集合。该集合记录了活跃用户的位置信息，最后再利用最小二乘法便可以获得活跃用户的传输信息，实现多用户的检测。该算法的具体步骤如下：

3 仿真结果

该部分考虑了在不同天线数目下，信噪比及过载率对检测性能的影响。其中过载率定义为：γ=K/N。设置总用户数K=150个，信道矩阵元素是独立的且满足H_n，k∈CN(0，1)，扩频序列是伪随机噪声序列(PN)，采用的调制方式为QPSK。当天线数目N_B=1时，假设系统中的噪声已知，并将算法称为理想SAMP算法。当天线的数目N_B=4时，所提算法中的m取3。

图1显示了不同天线数目下信噪比对误码率性能的影响，其中活跃用户的数量k=15，子载波数N=100，即过载率为150%。由图1知，在信噪比较低时，由于噪声的干扰，检测效果普遍偏差；随着信噪比的增加，检测效果逐渐变好。同时，随着天线数目的增加，系统的检测性能逐渐变好，所提算法提高了用户活动信息检测的准确性。

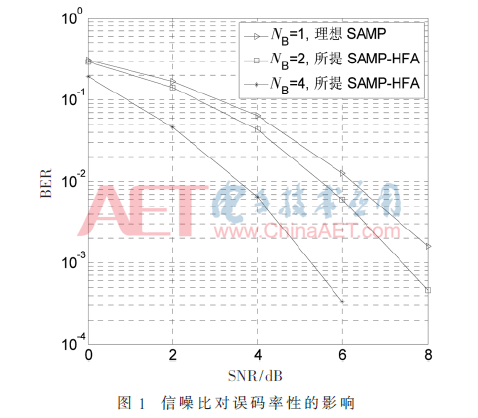
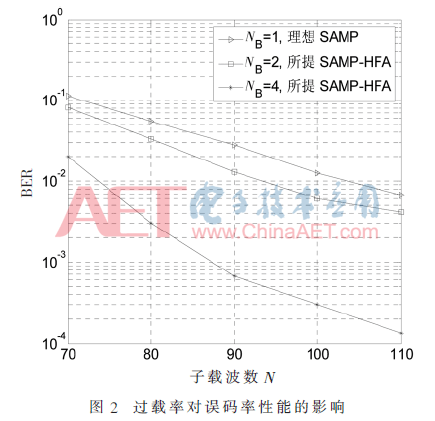
图2显示了不同天线数目下过载率对误码率性能的影响，其中假设活跃用户的数量仍为15个，系统的信噪比为SNR=6 dB。由图2可知：随着子载波数量的增加，即随着过载率的减小，理想的SAMP算法与所提的SAMP-HFA算法的误码率性能都逐渐提高，当天线数目N_B=4时，即使过载率较大，效果也比天线数目少时好很多。因此，可以达到节约频谱资源的目的。

4 结论

本文考虑了上行免调度NOMA系统中基站端配备多根天线的情况，并提出了一种稀疏度自适应的多用户检测算法SAMP-HFA。该算法解决了传统的基于压缩感知的多用户检测中活跃用户数量未知这一实际问题，它通过融合多根天线上检测出的用户活动信息，提高了活跃用户集合检测的正确性，进而提高了用户数据检测的正确性。仿真结果表明，该算法在信噪比以及过载率方面与单天线时相比，检测性能均有所提升。

参考文献

[1] WEI C，LIU H P，ZHANG Z C，et al.Approximate massage passing based joint user activity and data detection for NOMA[J].IEEE Communications Letters，2017，21(3)：640-643.

[2] DAI L L，WANG B C，YUAN Y F，et al.Non-orthogonal multiple access for 5G：solutions，challenges，opportunities，and future research trends[J].IEEE Communications Magazine，2015，53(9)：74-81.

[3] DING Z G，ADACHI F，POOR H V.The application of MIMO to non-orthogonal multiple access[J].IEEE Transactions on Wireless Communications，2016，15(1)：537-552.

[4] WANG B C，DAI L L，MIR T，et al.Joint user activity and data detection based on structured compressive sensing for NOMA[J].IEEE Communications Letters，2016，20(7)：1473-1476.

[5] HONG J P，CHOI W，RAO B D.Sparsity controlled random multiple access with compressed sensing[J].IEEE Transactions on Wireless Communications，2015，14(2)：998-1010.

[6] SHIM B，SONG B.Multiuser detection via compressive sensing[J].IEEE Communications Letters，2012，16(7)：972-974.

[7] WANG B C，DAI L L，ZHANG Y，et al.Dynamic compressive sensing based multi-user detection for uplink grant-free NOMA[J].IEEE Communications Letters，2016，20(11)：2320-2323.

[8] WANG B C，DAI L L，YUAN Y F，et al.Compressive sensing based multi-user detection for uplink grant-free non-orthogonal multiple access[C].Vehicular Technology Conference.IEEE，2016：1-5.

[9] DAI W，MILENKOVIC O.Subspace pursuit for compressive sensing signal reconstruction[J].IEEE Transactions on Information Theory，2009，55(5)：2230-2249.

[10] DO T T，GAN L，NGUYEN N，et al.Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C].2008 42nd Asilomar Conference on Signals，Systems and Computers.IEEE，2008：581-587.

[11] MALEKI S，CHEPURI S P，LEUS G.Optimal hard fusion strategies for cognitive radio networks[C].2011 IEEE Wireless Communications and Networking Conference.IEEE，2011：1926-1931.

[12] SUN C H，ZHANG W，LEAIEF K B.Cluster-based coop-erative spectrum sensing in cognitive radio system[C].2007 IEEE International Conference on Communications.IEEE，2007：2511-2515.

作者信息:

赵晓娟1，杨守义1，张爱华2，李晓宇1

（1.郑州大学 信息工程学院，河南 郑州450001；2.中原工学院 电子信息学院，河南 郑州450007）