0 引言

滚动轴承素有旋转机械设备的关节之称，其健康情况关系着整套设备的运转。磨损、过载、过压等原因使滚动轴承形成缺陷时，会使机器振动异常发出噪声，严重时会造成工业事故，耽误生产过程，因此对滚动轴承的故障诊断就有着重要的研究价值^[1]。

随着科技的发展，滚动轴承故障识别诊断的水平也有了很大的提升^[2-4]。文献[2]利用小波包变换的特点提取故障特征，并结合极限学习机实现了故障的正确分类。文献[3]利用离散Meyer小波对滚动轴承振动信号进行降噪，然后再使用支持向量机(Support Vector Machine，SVM)进行故障分类。文献[4]使用经验模态分解算法对提取的信号进行处理，提取出体现故障特征的敏感成分，借助谱峭度构建包络谱，完成故障诊断。

在前人研究的基础上，针对滚动轴承故障早期阶段故障特征信息微弱，一般方法难以高效地实现诊断故障冲击成分的特征提取，本文借助最大相关峭度(Maximum Correlated Kurtosis Deconvolution，MCKD)对滚动轴承故障信号进行特征提取，并提出利用改进的布谷鸟搜索（Improved Cuckoo Search，ICS）算法优化最小二乘支持向量机(Least Squares Support Vector Machine，LSSVM)参数，将优化后的LSSVM用于滚动轴承的故障诊断。

1 故障诊断模型

1.1 最大相关峭度解卷积算法

MCKD算法依赖信号的相关峭度最大化，借助信号中隐藏的冲击成分具有的周期性，利用解卷积运算增强信号中被各类噪声淹没的故障周期脉冲，因此在提取信噪比低的轴承早期故障信号中具有良好的效果^[5]。

通过传感器采集的轴承故障的振动信号为：

式中f为滤波系数。

1.2 改进的最小二乘支持向量机算法

LSSVM将最小二乘线性理论引入到SVM中，利用二次规划来解决函数估计问题^[8]，根据经验风险与置信范围最小化的原则，使算法具有较高的泛化能力。LSSVM故障诊断性能的优劣，实则取决于核函数参数σ以及惩罚因子C，这样对算法诊断过程的优化就转化为对这组参数的寻优。

布谷鸟搜索（Cuckoo Search，CS）算法是依据布谷鸟种群巢寄生的繁衍策略，通过鸟类特殊的飞行方式寻找最优的孵化的鸟蛋，此行为可以达到有效的参数寻优目的^[9-10]。算法的本质是使用新解与更优解比较来替换之前劣质的解。

2 故障诊断参数寻优的改进

2.1 识别概率Pa的改进

当CS算法参数发现概率P_a在[0.1，0.75]之间时，其全局搜索性随迭代次数的增长而逐步增加^[11]。因此在P_a合适的范围内，采用动态自适应机制改进发现概率P_a：

2.2 自适应步长的改进

为使自适应的效果不依赖人为设定的经验数值，减少由Lévy飞行随机决定搜索步长带来的影响，并处理好全局寻优能力与寻优精度的关系如下^[12]：

式中，n_i表示第i个鸟巢位置，n_best表示最佳的鸟巢位置，d_max表示鸟巢最佳位置与其余位置的最远距离值。在此基础上提出自适应调整步长策略：

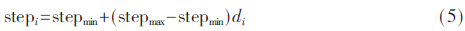
式中，step_max与step_min表示搜索最大与最小步长。本次迭代的步长可以凭借上次的迭代结果来自动更新，最后令α=step_i成立。至此，得到自适应步长的表达式，通过计算确认最优的参数σ以及惩罚因子C的组合。

3 故障诊断步骤

将平台采集的振动信号进行特征提取，得到的特征数据按类分组，作为实验模型的训练样本与测试样本。模型在学习过程中，利用ICS算法寻找最佳的参数组合，提高诊断的准确性，具体故障诊断的步骤如下，流程图如图1所示。

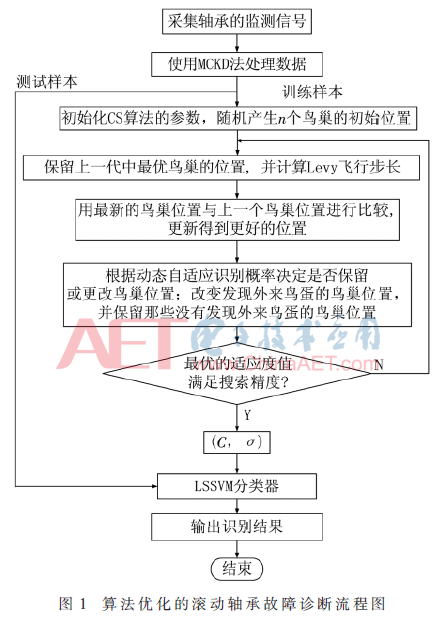
4 实验

4.1 MCKD对信号的特征提取

振动信号取自Case Western Reserve大学滚动轴承数据库，实验平台由主电机、实验轴承、信号采集的传感器以及控制器等元件组成。平台使用SKF轴承，系统的采样频率为20 kHz，采样长度为8 192，电机转速为1 797 r/m。轴承结构参数如表1所示。

实验采集了4种运行状态下滚动轴承的振动信号，分别为轴承的滚动体剥落信号、内圈剥落信号、外圈剥落信号以及正常运转下的振动信号。波形如图2所示，可以看出这4类振动波形中存有冲击成分，但这些冲击响应规律不明显，谱图分析看很难判别待测试信号(图2（e）)为哪一种运行状态，这给实验带来困难。

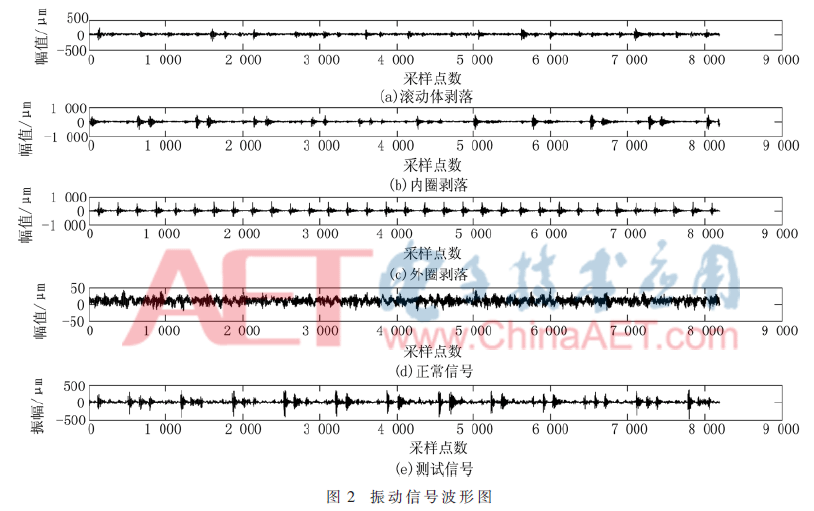
利用MCKD对这4类信号进行特征提取，由于MCKD进行信号特征提取的步骤相同，本文重点介绍外圈剥落信号，如图3（a）所示，按步骤(1)方法提取信号中的特征信息，如图3（b）所示。对比输入信号与MCKD处理后的信号，可以看出信号中的噪声干扰被滤除，淹没在噪声中微弱的脉冲冲击响应得到增强，信号周期可寻，在有限迭代次数的前提下，降低数据维数，提取出信号的特征信息。

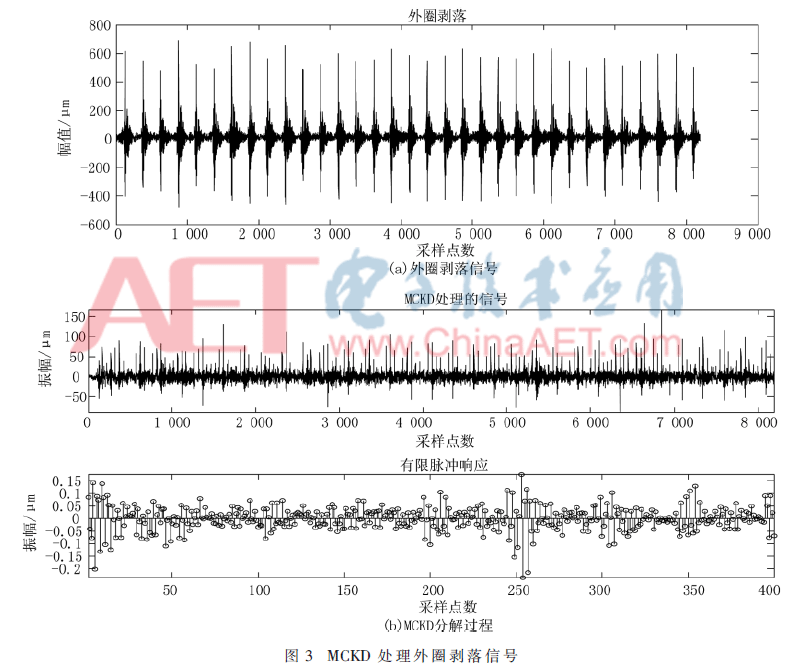
4.2 改进的布谷鸟算法参数寻优对比

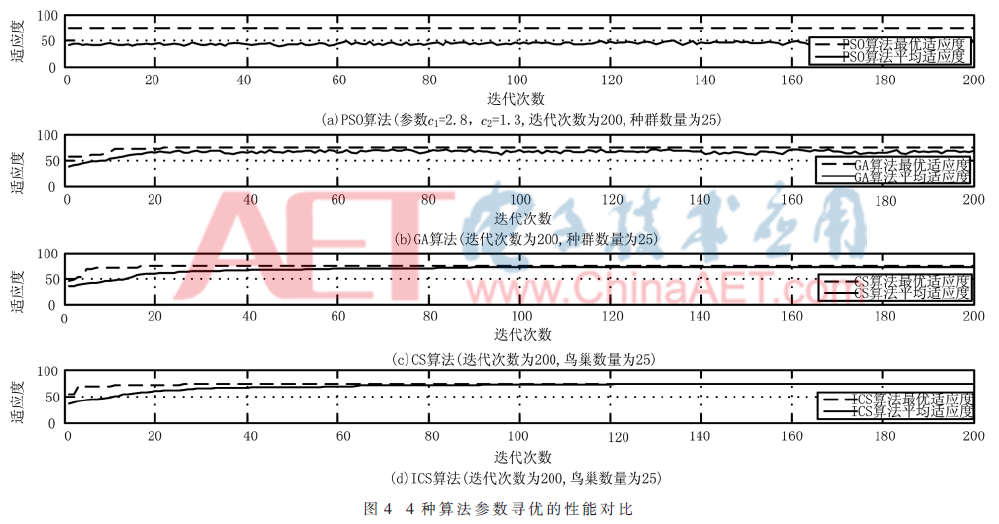
为验证ICS在参数寻优方面的优越性，选择粒子群优化算法(Particle Swarm Optimization，PSO)、遗传算法(Genetic Algorithm，GA)以及标准CS算法进行参数寻优的性能对比。各类算法寻优对比如图4所示，算法在参数寻优过程中，迭代次数都选择200次，PSO算法学习因子参数c₁=2.8，c₂=1.3，种群数量与GA算法一致，为25；CS算法与ICS算法，鸟巢数量也为25。由寻优曲线可以看出ICS算法在寻优速度方面比其他算法更快，收敛精度也更高，适应度也比其他算法更加稳定，所以ICS算法对LSSVM的参数寻优能力更强，得到的数据也更可靠。

4.3 故障诊断

利用MCKD算法对滚动轴承的4种状态的信号进行特征提取，得到了不同状态下的轴承振动特征信号的脉冲响应，这些脉冲响应作为LSSVM的样本集。实验中，4种振动特征信号每种有16组，共有64组数据。预处理后将这4种特征数据按种类标注为1、2、3、4，随机选取每种特征信号的8组作为LSSVM模型的输入，剩下的8组作为模型的测试样本，则有32组训练，32组测试。根据诊断识别步骤流程，进行ICS算法对LSSVM的参数寻优，得到最终的C为11.872 9、σ为8.785 0，通过LSSVM分类器将测试信号样本进行识别，在设定精度为1%的情况下，得到的识别结果如图5所示。同样将这64组数据样本应用到其他算法进行故障诊断识别，得到的诊断识别结果如表2所示。

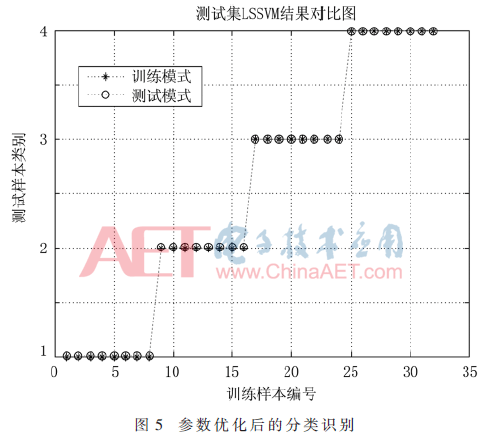
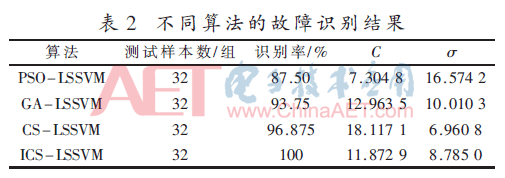
由图5和表2可以看出，在故障类别确定的情况下，利用ICS改进后的LSSVM滚动轴承故障的诊断方法与其他3种优化方法相比，诊断的识别率有所提高，诊断效果要高于其他算法，提出的方法是可行的。

5 结论

本文提出了一种将MCKD与改进优化的LSSVM相结合的算法，将其应用于滚动轴承故障诊断识别领域，通过实测数据分析得到以下结论：

（1）MCKD解决了提取微弱故障振动信号的难题，在有限迭代次数情况下，可增强噪声干扰下的轴承的振动信号，并提取特征信息；

（2）改进的算法在最优参数的搜索速度以及收敛精度性上要高于其他学习算法，可推广使用；运用在滚动故障诊断识别上具有良好的效果，可为滚动轴承故障诊断及时准确地维修提供技术支持。

由于实验使用的轴承故障类别有限，虽实现诊断准确率100%，但其适应性还有待提高，所以接下来的工作就是增加样本的故障类别，进一步提高算法的适应性，以满足实际应用的需要。

参考文献

[1] 张美玲，胡晓.基于LCD和改进SVM的轴承故障诊断方法[J].电子技术应用，2016，42(6)：81-83，86.

[2] 程文韬，邓芳明，郝勇，等.基于小波和ELM的电路故障诊断方法研究[J].仪表技术与传感器，2016(7)：89-92.

[3] ABBASION S，RAFSANJANI A，FARSHIDIANFAR A，et al.Rolling element bearings multi-fault classification based on the wavelet denoising and support vector machine[J].Mechanical Systems and Signal Processing，2007，21(7)：2933-2945.

[4] 蔡艳平，李艾华，石林锁，等.基于EMD与谱峭度的滚动轴承故障检测改进包络谱分析[J].振动与冲击，2011，30(2)：167-172.

[5] 唐贵基，王晓龙.自适应最大相关峭度解卷积方法及其在轴承早期故障诊断中的应用[J].中国电机工程学报，2015，35(6)：1436-1444.

[6] 唐贵基，王晓龙.基于包络谱稀疏度和最大相关峭度解卷积的滚动轴承早期故障诊断方法[J].中国机械工程，2015，26(11)：1450-1456.

[7] 宋玉琴，朱紫娟，姬引飞.基于粗糙集优化的信息融合故障诊断系统[J].电子技术应用，2015，41(8)：143-145.

[8] 张朝龙，江巨浪，江善和，等.基于改进PSO算法的LSSVM入侵检测模型[J].电子技术应用，2010，36(10)：132-135.

[9] 肖辉辉，段艳明.基于差分进化的布谷鸟搜索算法[J].计算机应用，2014，34(6)：1631-1635.

[10] YANG X S，DEB S.Cuckoo search via levy flights[C].World Congress on Nature & Biologically Inspired Computing.IEEE，2009：210-214.

[11] 王庆喜，郭晓波.基于莱维飞行的粒子群优化算法[J].计算机应用研究，2016，33(9)：2588-2591.

[12] 贺兴时，李娜，杨新社，等.多目标布谷鸟搜索算法[J].系统仿真学报，2015，27(4)：731-737.

作者信息:

刘 波，易 辉，薄翠梅，庄城城

（南京工业大学 电气工程与控制科学学院，江苏 南京211816）