0 引言

在开云棋牌官网在线客服行业中，多核处理器片上系统(Multiprocessors System-on-Chip，MPSoC)的设计是一个明显的趋势，根据国际开云棋牌官网在线客服技术蓝图预测^[1]，在2025年MPSoC上可能达到集成1 000个处理核心的众核的规模。日益增加的核心数目引出了一个重要的问题：系统的可扩展性。尽管采用片上网络能够提供一定的可扩展性，众核芯片的片上资源还需要有效管理以提供预期的性能^[2]。传统的管理方案采用集中式管理，然而这种单一管理者的模式在片上核心数目逐渐增多时会遇到瓶颈，因为该管理核心的计算任务将会变得极为庞大，而且由于其需要与片上所有其他核心进行通信，会导致其周围形成通信的热点(hot-spot)区域^[3-5]。

为了解决多核管理带来的问题，GUANG L等人提出了一种层次化的自监测方法^[2]，他们把监测划分为第三个维度，在原有的系统中添加监测层，使系统可以自我感知和自我管理，然而并没有对片上的簇具体如何划分给出算法，而且平台管理者需要完成所有的任务调度，其实际的计算任务依旧很大。Ana gnos topoulos.I等人提出了基于应用的实时分簇方案，当有新应用提出运行请求时，一个负责分簇的任务被激活，该任务获取应用的需求并依次将整个网络划分为簇，此时，与应用需求匹配的簇被选中，并由该簇内的一个区域管理者完成映射算法。MANDELLI M等人在此层次化结构上进行了改进^[4]，提出了三级管理方案。不同于之前提出的基于应用的动态实时分簇，他们提出了一种固定的片上分簇管理模式。全局管理者从应用池中获取待执行应用的信息，并将其转包给有空余计算资源的局部管理者，具体的任务映射由LMP对其从属核心进行，其分簇方案采取固定簇尺寸的分簇，GMP作为比LMP高一级的管理者，同样也要执行LMP全部的工作并且还对LMP进行管理。这种管理结构将任务映射从单一的GMP转移到了多个LMP上，加快了任务映射的速度，也减轻了GMP的任务量，但是固定分簇管理模式并没有考虑在片上发生核心损坏时的容错方案。

本文在MANDELLI M等人所提出的层次化结构以及固定分簇的基础上，加入了核级容错机制的设计，其中包括初始片上分簇管理方案，以及动态重分簇方案的设计。

1 NoC分簇方案设计

1.1 层次化管理方案设计

为了提高众核芯片的可扩展性，采用层次化管理方案，如图1所示。第一级核心负责整个系统的监测,并且执行簇的选择，将待执行应用转包给第二级核心。第二级核心完成具体的任务映射，同时逐级返回任务分配请求给GM(Global Manager)，GM完成最终的任务分配。当有新应用向系统提出执行请求时系统首先通过应用池(Application Repository)将应用的需求提供给第一级核心GM，GM根据第二级核心LM(Local Manager)反馈的系统资源占用情况，选择LM进行转包，LM完成对其下属的第三级核心PE(Processing Element)的任务映射。考虑到芯片上初始簇划分的规整性，决定将全局管理者作为一个特殊的局部管理者来使用。

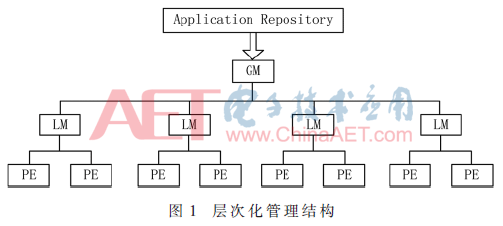
1.2 参数定义及选择

(1)相对管理开销

对于本文所采用的分簇管理方案，片上核心中只有部分核心能够处理用户任务，而一部分核心需要承担系统的管理任务。这里定义系统的相对管理开销p为式(1)：

其中，M为非管理核心数目，N为片上所有可用核心数目。

(2)曼哈顿距离(Manhattan Distance，MD)

对于采用2D Mesh拓扑结构的网络，对于片上坐标分别为(a，b)，(c，d)的两个IP核t_ab和t_cd，它们的曼哈顿距离等于两个核之间的最小跳步数为式(2)：

(3)平均曼哈顿距离(Average Manhattan Distance，AMD)

为了表示某个簇的聚拢程度，定义簇的平均曼哈顿距离。簇内每个核心到其他核心的曼哈顿距离的平均值求出后，再对这些均值求平均，即得到簇的平均曼哈顿距离。设簇内有n个核心t₁，t₂，…，t_n，则该簇的平均曼哈顿距离为式(3)：

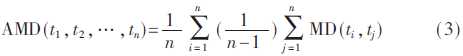
(4)全局管理者的放置

作为唯一与外部设备相连的处理核心，通常被放置在芯片的某一角，此处选择放在左上角。

(5)簇尺寸的确定

由于簇尺寸大小直接关系到片上相对管理开销的大小。一般而言，相对管理开销在15%以下，平均曼哈顿距离在3以下都是可以接受的范围，这里选择3×3的簇尺寸。

(6)局部管理者的放置

局部管理者的位置关系到簇内通信的效率,对于簇内不同位置的核心，其距离簇内其他核心的曼哈顿距离的平均值如表1所示。为提高簇内的通信效率，将局部管理者设置在簇的中间位置。

(7)容错问题的提出

在片上一些处理核心损坏之后，系统的每个簇也就变得不规整，所以需要对簇区域进行重新划分，即重分簇。当系统的可用处理核心数目减少，而簇的数量并没有减少以及簇管理者的数目没有减少，这就导致了系统管理开销的上升，而当损坏的核心数目达到一个簇的容量时，可以通过删除一个簇来降低系统的管理开销。即当前簇的数量为n，簇容量为s，当前正常工作的核心数量为Na，若：

则删掉一个簇。

(8)通信功耗模型

通常对于NoC的通信功耗采用按位计量能量模型。对于片上任意一条有向的边(directed edge)e_ij，每传输一位数据所消耗的能量为式(5)：

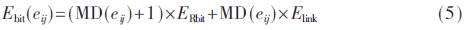
MD(e_ij)为核心v_i到v_j的曼哈顿距离，E_Rbit代表每传输一位数据在路由上(包括交叉式开关和读写缓冲区)所消耗的能量，E_link代表每传输一位数据在链路上所消耗的能量，E_Rbit和E_link对于某个给定的芯片均为常数。由式(5)可以看出，片上通信功耗与通信节点间的曼哈顿距离正相关。

(9)计算核心损坏概率模型

对于片上的计算核心的损坏概率，单个核心的损坏概率可以采用美国国防部发布的《电子设备可靠性预计手册》中所定义的模型加上Arrhenius模型中引入的温度参数对原模型进行的修正，可得：

其中E为过程中的激活能，K是玻尔兹曼常数，T是绝对温度。A为一常数，其取值应当使核心在正常工作温度下每周期的损坏概率在10^-9。

2 片上重分簇方案设计

2.1 簇区域重划分算法设计

整个重分簇方案分两步进行:对片上的簇进行重新划，对全局管理者和簇内的局部管理者进行重新选举。通常的解决方法是采用启发式算法,这里采用的算法是基于现有的分簇结果来进行重分簇，单个簇的填充采用贪心算法，簇区域重划分算法流程图如图2所示。

2.2 簇填充策略及遍历顺序设计

在2D Mesh下，每个簇的最优形状应该是正方形或逼近正方形，大小应当越小越好，才能保证簇的平均曼哈顿距离为最小，这即为贪心算法使用时的最优量度标准。

本文中对于某一个尚未填充满的簇，首先将覆盖簇内所有核心的最小的矩形划分出来，如果矩形内有尚未分簇的处理核心，优先将这些核心填充进簇内，若该矩形内核心已全部填充完毕，但簇仍未被填满，此时将该矩形进行扩展，此时又有两种情况。若矩形区域已为正方形，则将该区域向上下左右四个方向中的任意一个方向扩展均可；若矩形区域不是正方形，则对于该区域较长的那一对边所对应的方向进行扩展，使得整个矩形的区域向正方形逼近经过每一次扩展，矩形区域内都有可能出现新的尚未分簇的处理核心，依次将这些核心填充进当前簇直至填满,这种单个簇填充策略是一种保证先填充簇的结构最优化的策略。

片上簇填充的遍历顺序依据上节提出的单个簇填充策略，对片上已有的所有簇进行遍历，须遵循一定的顺序。这里采用一种以左上角为起点的折线形的顺序来遍历整个芯片，定义初始的横向和纵向扩展方向分别为向右和向下。

2.3 局部管理者的选举

由于区域重新划分后，原有的任务映射结构被改变，各个簇与全局管理者的通信量难以进行采样，此时对于局部管理者的选举可以忽略掉全局管理者的影响。

而片上的通信功耗依据按位计量能量模型^[6]，每跳步数耗能量与传输数据的位数成正比。要降低簇内通信功耗，必须要求局部管理者到簇内其他处理核心的跳步数最少，即距离其他核心的曼哈顿距离之和为最小。

由于簇内核心数目不是很多，这里可以采用穷举搜索的方法，以确定簇内距离其他核心的曼哈顿距离之和最小的核心，将其选举为局部管理者。之前标记过的簇由于含有全局管理者，所以不参与局部管理者的选举。

3 实验结果及对比分析

3.1 与随机分簇算法的比较

随机分簇算法采用与区域重划分算法有相同的遍历顺序，不同的是其在填充核心时是随机选择剩余可用核心进行填充。

由前述的核心损坏模型可知，核心的损坏概率为常数，为了实验的方便，本文将损坏概率设置为1/100。分别利用区域重划分算法与随机分簇算法进行分簇，并计算每次分簇后芯片的平均曼哈顿距离。芯片的平均曼哈顿距离由式(7)给出，其中c_i表示第i个簇，为c_i内可用核心数目，N为片上所有可用核心数目。

基于9×9的芯片与3×3的簇尺寸，进行了故障注入实验,通过10 000次的分簇实验，区域重划分算法的执行结果基本都在2.2以下，最高仅达到了2.35。而随机分簇算法，其平均执行结果在2.4到2.6左右，最高达到了3.5左右。

将这10 000次的分簇结果取平均，结果如表2所示，区域重划分算法比随机分簇算法AMD_chip平均值减少3.9%，区域重划分算法的执行结果要优于随机分簇算法。

为了验证区域重划分算法对于较多核心损坏时是否能够有较好的分簇结果，本文进行了不同数目的故障注入。损坏概率仍然设置为1/100，对于一个众核芯片而言，损坏20%以上的核心认为是比较严重的损坏，注入时的数目选取1到20个故障(1.2%-24.7%)来进行实验，注入完成后分别利用区域重划分算法与随机分簇算法进行分簇，并计算每次分簇后芯片的平均曼哈顿距离，分簇后所得的结果对比如图3所示，可以看出区域重划分算法明显优于随机分簇算法。

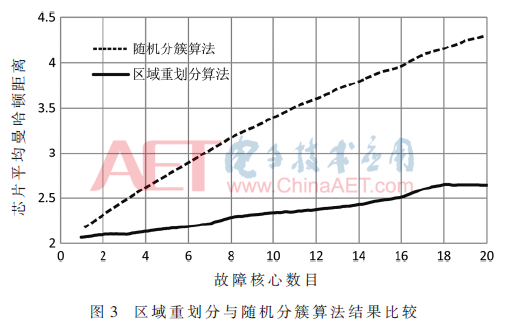
3.2 与冗余核行列替换策略的比较

实际工程中，为了保证芯片能够实现核级的容错，片上的冗余核是必不可少的，这里采用工程上常用的行列替换的冗余核替换策略与本文提出的区域重划分算法进行比较。

冗余核行列替换策略采用距离最近的冗余核进行替换。本文在芯片的最右侧那一列放置一列共计9个冗余核，将损坏概率设置为1/100，进行10 000次随机注入，分别利用区域重划分算法与横向冗余核替换策略进行实验，并计算每次分簇后芯片的平均曼哈顿距离，将10 000次的结果取平均，结果如表3所示，区域重划分算法比行列替换算法AMDchip平均值减少1.85%。

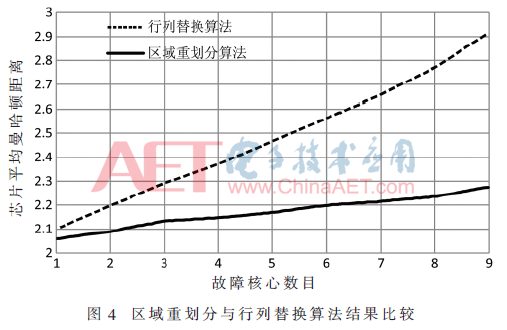
与3.1类似，进行不同数目的故障注入，损坏概率仍然设置为1/100，由于只放置了9个冗余核，故注入故障数目为1到9，每种数目的故障进行500次随机注入。注入完成后分别利用区域重划分算法与行列替换算法进行分簇，并计算每次分簇后芯片的平均曼哈顿距离，分簇后所得的结果对比数据如图4所示，可以看出区域重划分算法优于行列替换算法。

4 结论

本文针对众核芯片的片上资源划分和管理问题，基于固定分簇方案加入核级容错机制的设计，设计了区域重划分算法，以平均曼哈顿距离为约束目标，利用MATLAB实现了该区域重划分算法，模拟实验结果表明，该算法的平均曼哈顿距离比随机分簇算法和冗余核行列替换算法都要小，而且在故障注入数目较多的情况下，所得的平均曼哈顿距离相比其他两种算法具有显著的减少，采用此算法可以降低NoC的通信功耗，具有实际应用价值。

参考文献

[1] VAJDA A.Programming Many-Core Chips[M].Springer US，2011.

[2] GUANG L，NIGUSSIE E，RANTALA P，et al.Hierarchical agent monitoring design approach towards self-aware parallel systems-on-chip[J].Acm Transactions on Embedded Computing Systems，2010，9(3)：177-185.

[3] LIAO X，SRIKANTHAN T.A scalable strategy for runtime resource management on NoC based manycore systems[C]//International Symposium on Integrated Circuits.IEEE，2011：297-300.

[4] MANDELLI M，CASTILHOS G M，MORAES F G.Enhancing performance of MPSoCs through distributed resource management[C]//IEEE International Conference on Electronics，Circuits and Systems，2012：544-547.

[5] CHOU C L，MARCULESCU R.FARM：Fault-aware resource management in NoC-based multiprocessor platforms[J].Design Automation & Test in Europe，2011：1-6.

[6] YE T T，BENINI L，DE MICHELI G.Analysis of power consumption on switch fabrics in network routers[M].2002.