0 引言

惯性传感器作为惯性导航系统中的核心部件，其精度直接影响到整个惯导系统的性能。随着科学技术不断发展，对精度要求越来越高^[1]，因此，如何提高惯性传感器精度是长期以来的研究重点。目前主要通过滤波的方式提高惯性传感器的精度。传统处理方法有小波分析和卡尔曼滤波^[2-3]等。这些方法均从变换域表示来获取信号的属性，针对特定类型的特定信号取得较好的效果，不具有普遍性。近年来，稀疏性问题随着压缩感知理论^[4]的提出得到了系统性的研究，并运用于信号去噪领域。由于大部分信号在变换基下是稀疏的，所以该方法得到广泛的应用。文献[5]通过K-VSD算法训练获得冗余字典，再利用稀疏表示实现惯性传感器信号滤波，不过原子库数目巨大。此外，基于稀疏分解理论的主要重构方法是正交匹配追踪算法(Orthogonal Matching Pursuit，OMP)^[6]，但运行时间较长。压缩采样匹配追踪算法^[7]虽然改善了重构速度，但要求在给定迭代次数的条件下进行，且需已知信号的稀疏度。目前，随着智能算法的兴起，文献[8]提出人工蜂群与MP重构算法结合，通过模拟蜂群采蜜以加速最优化进程，不过该算法更新公式单一，易陷入局部最优。遗传算法与重构算法结合^[9]相继提出，交叉、变异等遗传算子很好地丰富了种群，但所需种群数多，收敛速度慢。

针对现有算法的缺陷，本文提出将免疫量子进化与OMP相结合来实现惯性传感器信号重构。该算法无需已知信号稀疏度，通过免疫机制中的免疫操作，不断增加抗体对抗原的亲和度，从而找到最优解。算法中，量子搜索机制可有效防止算法后期的退化现象，加快OMP算法的收敛速度。引入免疫机制使量子进化算法具有更强的全局搜索能力，不易陷入局部最优状态，并有效保证了信号的重建速度和精度。

1 算法理论

1.1 量子进化算法理论

量子进化算法^[10]是一种基于量子计算原理的优化方法。该算法以量子计算为基础,引入量子比特编码和量子门。量子比特编码是用量子态矢量表示染色体，一条染色体能表达为多个态的叠加。量子门使种群得到更新，保证收敛性。所以量子进化与经典遗传算法相比，拥有丰富的多样性特征和较好的收敛性。

量子状态用量子比特表示，与经典比特不同之处在于叠加态的存在，它可以落在|0>和|1>之外的线性组合态。量子位状态用下式表示：

1.2 OMP算法原理

当信号长度有限时，随着k值的不断增大，信号残余的能量将以指数形式递减，最后收敛到0。

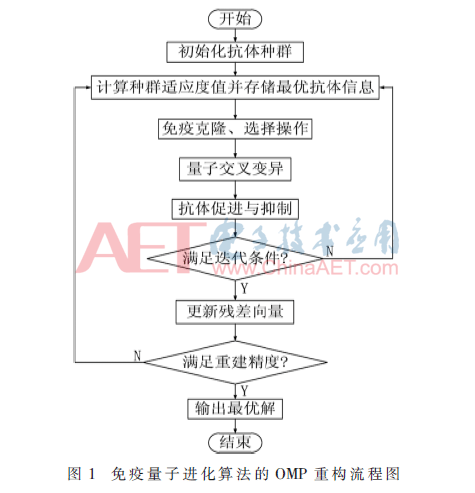
2 免疫量子进化算法的OMP重构方法

将免疫量子进化算法与OMP重构结合用于惯性传感器信号，通过构建与信号特征相匹配而与噪声信号不相关的匹配原子，组成过完备原子库。先在库中通过免疫操作和量子操作来加速最佳匹配原子搜索进程，提取与信号最匹配的原子；然后选取最大迭代次数作为迭代的终止条件，避免因迭代次数选取不当，影响处理效果；最后利用各次迭代提取的最佳匹配原子完成惯性传感器信号的重构，进而实现信号滤波。算法中以原子库作为种群、原子库的一个原子的参数组作为抗体，寻找适应度大的抗体作为优化目标，信号在原子库的投影值则为适应度函数值。

2.1 改进策略

本算法将量子搜索机制和免疫算法的克隆选择原理相结合，利用量子编码的叠加性构造抗体；通过克隆操作产生原始种群和子种群以实现种群扩张，提高了局部搜索能力，同时借助量子交叉操作避免陷入局部最优。基于克隆算子的基本框架，采用量子编码来表示抗体，设计针对量子编码的量子非门变异，并构造具有量子特性的多点交叉策略。

2.2 免疫操作

克隆：采用轮盘赌方法确定克隆产生的子种群规模。设克隆前种群为Q={q₁，q₂，…，q_N}，N为种群规模的大小，克隆操作后的种群为Q′={Q，C}，其中C为克隆产生的抗体子群。克隆规模主要依据抗体-抗原适应度，抗体中的相对大小可自适应调整，即抗体受抗原的刺激时，克隆规模的多少依据其影响的大小来确定。公式如下：

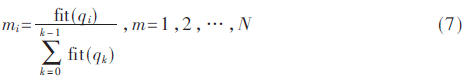
式中，m_i为种群中第i个抗体的克隆规模，fit(q_i)为第i个抗体-抗原的亲和度，即抗体i的适应度值。

选择：从克隆操作后的种群中选择优秀的抗体，形成新的种群。即通过计算适应度函数值选择最佳抗体集合，进而组成最优解集合。

2.3 量子操作

将抗体进行变异，即利用概率变异重新计算新抗体的适应度值，将一定数量亲和度高的解作为优秀抗体。

量子交叉：本文采用多点交叉。即：选出相互配对的两个抗体，随机设置多个交叉点，然后以交叉概率互换抗体中交叉点之间的基因以增加种群多样性。

2.4 抗体促进与抑制

计算种群中抗体的适应度值，并对种群中的抗体两两进行比较，将适应度值大的抗体替换适应度值低的抗体，以达到抗体的促进与抑制效果。

2.5 计算种群适应度

本文算法在搜索最优抗体的过程中，不依赖任何外部信息，仅以种群内部各个抗体的适应度函数值为线索进行搜索。文中定义信号或信号残余R_kf与原子的内积绝对值|kf，g_γk>|为适应度函数，记为Y_k:Y_k=arg|kf，g_γk>|(k=1，2，…，N)。

2.6 算法步骤

设Gabor原子库矩阵为M×N列，将该矩阵的N列作为N个抗体，每个抗体具有1个量子比特位，M个量子态，其中N个量子比特表示矩阵的N列，每个量子态表示矩阵的每个元素。步骤如下：

2.7实时处理方法

3 仿真与结果分析

3.1 静态数据的验证

首先用惯性传感器静态观测数据验证算法。通过引入信噪比、均方误差、标准差(零漂值)和处理时间对降噪效果进行评估。其中，均方误差为参数估计值与真实值之差平方的期望值，以衡量平均误差。仿真信号为某光纤陀螺(FOG)静态输出信号的实际采样，采样频率为5 000 Hz，信号长度N=300。设算法中交叉概率为0.85，变异概率为0.1，最大迭代次数为20。其中，以小波滤波后的信号作为该光纤陀螺的真实信号。经本文算法处理后的效果如图2所示。

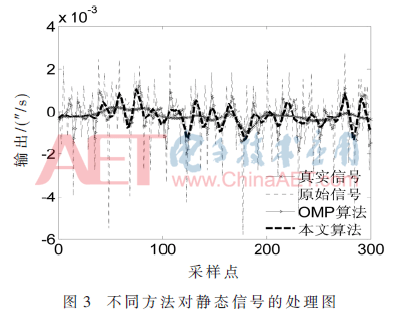
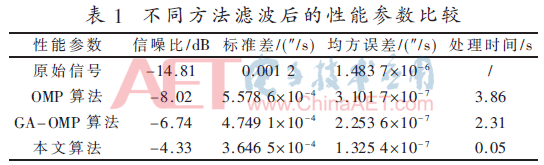
为了便于比较，将该算法与OMP及GA-OMP算法（遗传算法的OMP重构）在相同的实验环境下进行相同参数的实验。限于篇幅，仅列出OMP算法与本文算法的效果对比图，仿真结果如图3所示。统计同一静态信号处理后的性能参数，具体数据如表1所示。由表1可知，静态信号经本文算法处理后，性能参数均优于OMP及GA-OMP算法，且无需事先已知信号稀疏度。综合表1和图3可得，惯性传感器信号的实际静态信号中含有的噪声能量远大于真实信号，输出的零偏和波动性较大。经实验验证，OMP算法处理后，单点信号处理时间为12.8 ms，大于系统要求的0.2 ms(采样频率为5 000 Hz)，不能进行实时处理。本文算法与OMP算法相比，处理后信号信噪比提高3.69 dB，零漂值降低1.932 1×10^-4(″/s)，均方误差降低1.776 3×10^-7(″/s)。比原信号信噪比提高了10.48 dB，标准差降低了8.353 5×10^-7(″/s)，均方误差降低了1.351 2×10^-6(″/s)，且单点信号处理时间为0.166 ms，达到实时处理要求。实验结果表明，本算法大大缩短信号处理时间的同时，改善了零漂值，提高了信号处理精度，故验证了算法对惯性传感器静态信号的有效性。

3.2 对动态数据的验证

利用动态数据进一步验证算法的可行性。仿真信号为：通过高频滤波器取出某光电跟踪系统输出高于500 Hz的实际FOG信号，作为噪声叠加到正弦信号上。正弦信号频率为128 Hz，叠加的信号采样频率为5 000 Hz，信号长度N=300。其他参数与静态信号一致。本文算法处理后效果如图4所示。

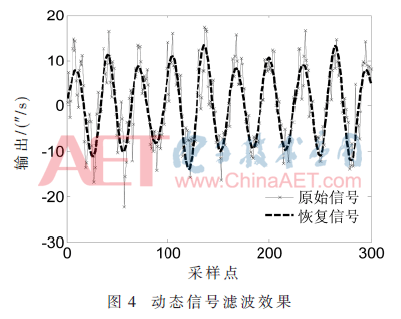
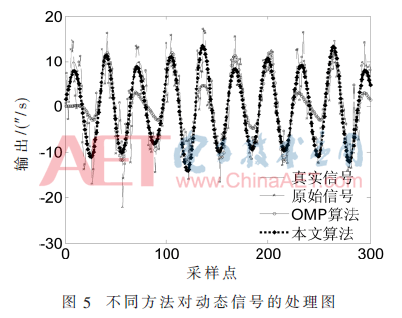
图5为相同实验环境和参数设置下OMP算法与本文算法的效果图。表2为本文算法与OMP及GA-OMP算法对同一动态信号处理后的性能参数比较。动态信号不存在零漂值，故不列出。由表2可知，本文算法在动态数据仿真测试下，性能仍优于OMP及GA-OMP算法。经实验验证，OMP算法处理后的时间为4.18 s，不能满足实时处理要求。经本文算法处理后，与OMP算法相比，信号信噪比提高了6.2 dB，均方误差降低了25.878 (″/s)。比原始信号信噪比提高了7.55 dB，均方误差降低了28.551(″/s)。有效改善了信号输出精度的同时，信号单点处理时间为0.133 ms，满足实时处理要求，因此，验证了算法对动态信号处理的有效性。

4 结论

本文根据惯性传感器信号的特点，将免疫机制引入量子进化算法对OMP重构算法进行改进，并将其应用于惯性传感器输出信号的实时处理。由仿真结果可知，在信号稀疏度未知的情况下，所提出的算法对惯性传感器的静态和动态数据均能在加快信号处理的同时提高滤波性能，为惯性传感器信号提供了实际应用价值和广泛的应用前景。

参考文献

[1] 许江宁，朱涛，卞鸿巍.惯性传感技术与展望[J].海军工程大学学报，2007，19(3)：1-5.

[2] 郭晓松，张东方，薛海建，等.基于小波去噪和TLS算法的全姿态寻北[J].系统工程与电子技术，2016，38(2)：362-367.

[3] 戴冬冰.基于卡尔曼滤波的陀螺仪数据处理[J].数字技术与应用，2014(5)：119-121.

[4] BOUGHER B.Introduction to compressed sensing[J].The Leading Edge，2015，34(10)：1256-1257.

[5] 蒋行国，张龙，许金海.一种基于稀疏表示的惯性传感器信号实时滤波方法[J].计算机应用研究，2015，32(5)：1480-1482.

[6] WU R，HUANG W，CHEN D R.The exact support recovery of sparse signals with noise via orthogonal matching pursuit[J].IEEE Signal Processing Letters，2013，20(4)：403-406.

[7] HUANG F，TAO J，XIANG Y，et al.Parallel compressive sampling matching pursuit algorithm for compressed sensing signal reconstruction with OpenCL[J].Journal of Systems Architecture，2016，27(1)：51-60.

[8] 侯坤，易正俊，何荣花.信号稀疏分解的人工蜂群-MP算法[J].计算机仿真，2012，29(11)：247-250.

[9] 王国富，张海如，张法全，等.基于改进遗传算法的正交匹配追踪信号重建方法[J].系统工程与电子技术，2011，33(5)：974-977.

[10] CAO G L，HU R，QIAN B.Effective hybrid quantum evolutionary algorithm for capacitated vehicle problem[J].J Comp Inte Manu Syst，2015，21：1101-1113.

作者信息：

蒋行国1，2，罗珍珍1，李海鸥1，2，欧少敏3

(1.桂林电子科技大学 信息与通信学院，广西 桂林541004；

2.桂林电子科技大学 广西精密导航技术与应用重点实验室，广西 桂林541004；

3.桂林电子科技大学 信息科技学院，广西 桂林541004）