0 引言

铁路长期演进(Long -Term Evolution for Railway，LTE-R)系统是极具前景的高速铁路通信系统。根据国际铁路联盟的规划，铁路移动通信系统将从传统的铁路全球移动通信系统(Global System for Mobile Communications-Railway，GSM-R)直接过渡到LTE-R系统^[1]。对于LTE-R系统，列车移动速度通常超过300 km/h，会产生严重的多普勒频移。同时，无线信道状态呈现动态变化特点。如何保证在高移动性场景下，仍然能够为用户提供可靠的无线通信服务，信道估计是关键。

信道估计问题已经引起了广泛关注。根据是否需要引入导频信息，信道估计可以分为盲信道估计、导频辅助信道估计和半盲信道估计。然而，盲信道估计^[2-3]虽然省去了导频信息的传递，提高了频带利用率，但其算法收敛速度较慢，且需要大量的数据存储和复杂的数学运算，因此局限应用于慢时变衰落信道，对数据实时处理要求不高的地方，不适用于高移动性信道估计；导频辅助信道估计^[4-5]具有较低的算法复杂度，便于系统的实现，且能实时跟踪CSI，适合进行快速时变信道估计；半盲信道估计算法^[6-7]虽然在复杂度和导频数量上进行了折衷，但复杂度仍然较高，也不适合对快速动态变化信道进行估计。基于基扩展模型(Basis Expansion Model，BEM)的导频辅助信道估计方法^[8-9]通过若干基函数与系数乘积和的方式，可以对快速时变信道进行近似，已经引起了广泛关注。因此，本文将采用BEM对高移动性信道估计问题进行研究。

本文针对LTE-R通信系统，开展高移动性场景的信道估计研究。首先，建立LTE-R系统的信道模型。然后，根据BEM将LTE-R信道冲激响应表示为若干基函数与系数乘积和的形式。接下来，通过对基函数系数进行估计的方式，实现对LTE-R信道的拟合。最后，通过仿真对4种形式的BEM进行性能评估。

1 LTE-R信道模型

高速铁路LTE-R通信系统结构如图1所示。设计分布式基站可以解决高速列车通信问题，分布式基站由室内基带处理单元（Building Baseband Unit，BBU)和射频拉远单元（Radio Remote Unit，RRU)组成^[10]。BBU位于基站的室内，RRU被部署在铁路沿线附近，多个RRU分别通过光纤将信号传输到BBU。分布式基站的设计可以扩大小区信号的覆盖范围，在一定程度上可以减少用户越区切换次数。BBU和RRU分别用于处理基带信号和射频信号，由于通过光纤将基带信号从BBU传输到RRU，从而避免了射频信号的长距离传输，可以显著降低传输损耗。此外，由于无线信号穿过列车车厢会造成严重的穿透损耗，为了保证RRU和列车之间的可靠通信，在列车的顶部安装一个车载台（Vehicular Station，VS）。VS通过无线方式与RRU建立连接。同时，在每节车厢里都安装一个中继器（Repeater，R），中继器通过有线方式与VS建立连接。车厢里的不同用户设备（User Equipments，UE）可以通过中继器连接到网络。

对于高速铁路LTE-R通信系统，由于RRU部署在铁路沿线附近，同时铁路沿线存在特殊的地理环境特征，使得RRU和VS之间除了存在一条直接的视距（Line-of-Sight，LOS）路径以外，还存在若干条间接的非视距（Non-Line-of-Sight，NLOS）路径。受文献[11]、[12]启发，将信道冲激响应表示为：

式中，σ是非视距信号归一化平均功率的标准偏差，A为视距信号的平均幅度。

2 基于基扩展模型的信道估计方法

2.1 基扩展模型信道建模

采用BEM进行信道建模的基本原理是通过若干基函数与系数乘积和来拟合无线信道。假设信号传播的多径数量为L，对于第l条路径，若N点采样的信道增益向量为h_l，同时基函数向量为b_m，那么，通过基扩展模型拟合信道增益h_l可以表示为：

此外，根据基函数形式的不同，基扩展模型可以分为多项式基扩展模型（Polynomial BEM，P-BEM）、复指数基扩展模型（Complex Exponential BEM，CE-BEM）、泛化复指数基扩展模型（Generalized CE-BEM，GCE-BEM）和优化泛化复指数基扩展模（OptimizationGCE-BEM，OGCE-BEM），分别介绍如下：

对于P-BEM是以泰勒级数为基础的，其第m个基函数第n个元素可以表示为^[13]：

式中，0≤n≤N-1，0≤m≤M-1。

对于CE-BEM，是以傅里叶级数理论为基础的，其第m个基函数第n个元素可以表示为^[14]：

对于OGCE-BEM，其第m个基函数第n个元素可以表示为^[16]：

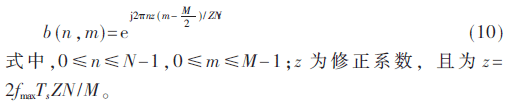
2.2 基函数系数估计

时变多径信道的输入输出响应关系式有：

式中，H为N×N维时域信道循环矩阵，且表达式为：

所以，频域Y表示为：

3 仿真结果和分析

图2对比了不同BEM的NMSE性能。在仿真中，移动速度是v=350 km/h，调制方式为64QAM，基函数个数为11。可以看到，GCE-BEM的性能优于CE-BEM，原因是GCE-BEM对多普勒频谱更加密集的采样能有效减少CE-BEM的频谱泄露问题。同时，OGCE-BEM的估计性能优于GCE-BEM，这是因为OGCE-BEM通过对GCE-BEM基函数频率的修正，减少了高频基函数对模型带来的误差，使信道估计性能达到最优，弥补了GCE-BEM在高频点的估计误差偏大问题。另外，P-BEM估计性能最差，说明依据泰勒级数理论基础的多项式线性组合的基函数模型对于LTE-R系统信道拟合误差偏大。

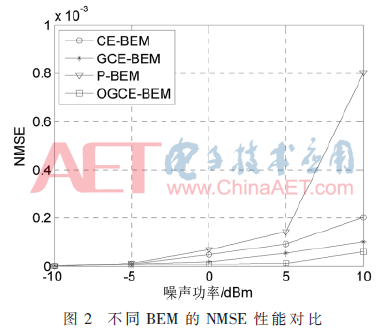
图3对比了不同移动速度时OGCE-BEM的NMSE性能。在仿真中，调制方式为64QAM，基函数个数为11。当移动速度为v=350 km/h，噪声功率为0 dBm时，OGCE-BEM的NMSE达到10^-5，说明即使在高阶调制情况下，采用OGCE-BEM进行高移动性信道估计，也能够获得较小的NMSE。

图4对比了不同基函数个数时OGCE-BEM的NMSE性能。在仿真中，移动速度是v=350 km/h，调制方式为64QAM。当基函数个数为3、噪声功率为10 dBm时，OGCE-BEM的NMSE仍然能够达到10^-4。当基函数个数为15、噪声功率为10 dBm时，OGCE-BEM的NMSE能够达到10^-5。通过增加一定的基函数个数，可以使信道估计的NMSE性能提高。

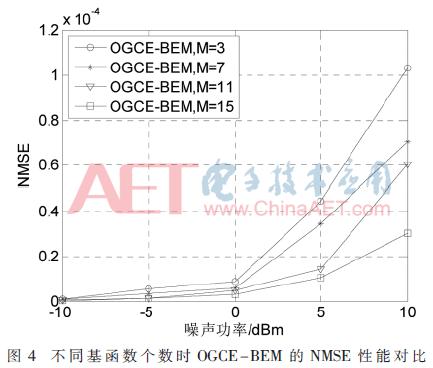
图5对比了不同调制方式时OGCE-BEM的NMSE性能。在仿真中，移动速度为v=350 km/h，基函数个数为11。当噪声功率为0 dBm时，OGCE-BEM的3种调制方式的NMSE都可以达到10^-6，且调制方式为QPSK时，OGCE-BEM的NMSE性能最优，其次是16QAM，64QAM最差。即使当噪声功率达到10 dBm时，64QAM的NMSE也能达到10^-5。

4 结论

本文研究了高移动性场景下LTE-R系统的信道估计问题。根据BEM，将信道冲激响应表示为一系列基函数与系数乘积和的形式。通过对基函数系数进行估计，实现对LTE-R系统的信道估计。由于本文只针对导频位置的信道状态进行估计，下一步将考虑插值算法，实现对数据位置的信道状态进行估计。同时，根据得到的估计误差，对基函数的个数进行动态调整。

参考文献

[1] HE R S，AI B，WANG G P，et al.High-speed railway communications：from GSM-R to LTE-R[J].IEEE Vehicular Technology Magazine，2016，11(3)：49-58.

[2] ZHOU S L，GIANNAKIS G B，SCAGLIONE A.Long codes for generalized FH-OFDMA through unknown multipath channels[J].IEEE Transactions on Communications，2001，49(4)：721-733.

[3] SONG S，SINGER A C.Blind OFDM channel estimation using FIR constraints: reduced complexity and identifiability[J].IEEE Transactions on Information Theory，2007，53(3)：1136-1147.

[4] BARHUMI I，LEUS G，MOONEN M.Optimal training design for MIMO OFDM systems in mobile wireless channels[J].IEEE Transactions on Signal Processing，2003，51(6)：1615-1624.

[5] LI Y，SESHADRI N，ARIYAVASITAKUL S.Channel estimation for OFDM systems with transmitter diversity in mobile wireless channels[J].IEEE Journal on Selected Areas in Communications，1999，17(3)：461-471.

[6] MEDLES A，SLOCK D T M.Semiblind channel estimation for MIMO spatial multiplexing systems[C].IEEE Vehicular Technology Conference，2001，2：1240-1244.

[7] MEDLES A，SLOCK D T M.Linear precoding for spatial multiplexing MIMO systems：blind channel estimation aspects[C].IEEE International Conference on Communications(ICC)，2002，1：401-405.

[8] RABBI M F，HOU S W，KO C C.High mobility orthogonal frequency division multiple access channel estimation using basis expansion model[J].IET Communications，2010，4(3)：353-367.

[9] LIU L，TAO C，QIU J H，et al.Position-based modeling for wireless channel on high-speed railway under a viaduct at 2.35 GHz[J].IEEE Journal on Selected Areas in Communications，2012，30(4)：834-845.

[10] ZHAO Y S，LI X，LI Y，et al.Resource allocation for high-speed railway downlink MIMO-OFDM system using quantum-behaved particle swarm optimization[C].IEEE International Conference on Communications(ICC)，2013：2343-2347.

[11] GUAN K，ZHONG Z D，AI B.Assessment of LTE-R using high speed railway channel model[C].Third International Conference on Communications and Mobile Computing(CMC)，2011：461-464.

[12] TKAC A，WIESER V，POLLAK S.Calculation of impulse response in rician and rayleigh channel[C].ELEKTRO，2012：99-102.

[13] HU D，WANG X D，HE L H.A new sparse channel estimation and tracking method for time-varying OFDM systems[J].IEEE Transactions on Vehicular Technology，2013，62(9)：4648-4653.

[14] TUGNAIT J K，HE S C，KIM H.Doubly selective channel estimation using exponential basis models and subblock tracking[J].IEEE Transactions on Signal Processing，2010，58(3)：1275-1289.

[15] KHAL R N，ZHANG J R，ZAKHAROV Y V.Robustness of joint bayesian frequency offset and channel estimation based on basis expansion models[C].Conference Record of the Forty-Third Asilomar Conference on Signals，Systems and Computers，Pacific Grove，2009：957-961.

[16] 张钦娟，武穆清，郭起霖，等.OFDM系统中优化的泛化复指数基扩展模型[J].西安电子科技大学学报，2012(3)：131-135.

作者信息:

黄锦锦，赵宜升，陈忠辉，赖鑫琳，董志翔

(福州大学 物理与信息工程学院，福建 福州350108)