张江波
(河北工程大学 信息与电气工程学院,河北 邯郸 056038)
摘要:为了提高在密集多径信道下信号检测性能,提出了一种基于稀疏表示的非相干检测方法。此方法考虑了稀疏表示的原理及特点, 以稀疏信号分解、主成分分析及特征信号提取为基础, 通过利用假设检验方法对信号进行最终判决, 实现了在密集多径环境下的信号检测。仿真验证了所提方案的可行性,对比了传统方案和所提方案的检测性能,结果表明该方法具有更好的检测能力。
关键词:信号检测;稀疏表示;非相干检测;密集多径信道
中图分类号:TN914文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.02.020
引用格式:张江波.基于稀疏表示的密集多径非相干信号检测方法研究[J].微型机与应用,2017,36(2):66-69.
0引言
随着通信技术的发展,未来无线通信技术不断向着高速传输方向迈进,移动通信网络标准逐渐迈向5G时代。在5G待选通信技术中,毫米波通信技术可能成为下一代移动通信的关键技术。其传输带宽由低频段增至高频段,大带宽具有扩频增益、降低信号辐射等优点,可以为大规模无线传感器网络、体域网、个域网等提供低功耗、绿色通信的解决方法,对未来无线网络的发展具有重要意义[1]。
在毫米波通信技术中,典型的应用场景常常是在室内完成,然而,当无线传输系统带宽超过500 MHz时,这种无线信号将呈现密集多径特性。由于室内存在着大量反射体,这种密集多径信号将非常复杂,给信号接收机的设计带来诸多难题。在传统的窄带/宽带系统中,通常包含3~10个多径信号,一般可以通过信道估计、Rake接收机进行信号处理[2],通过有效的分集增益减小多径带来的损耗,提高系统的性能。但是,在毫米波大带宽、密集多径的情况下,路径多达几十条至上百条。多径数量的急剧增加,使得接收机的采样频率高达数兆赫兹,大大增加了数模采样的功耗和对器件的要求,其相应的信道估计算法的复杂度也极高。此外,由于Rake接收机需要采用大量接收抽头进行合并,这种情况使得信号接收机的系统异常复杂,硬件要求极高而难以实现。
为了克服上述问题,文献[3]提出了简化密集多径信道下的带宽信号检测过程(TransmittedReference, T-R)的方案, 这种方案将第一个信号作为传送模板,在相邻的第二个信号上加载有用信息,然后对这两个信号做信号相关处理,实现了信道的有效估计和Rake接收。该方案虽然降低了密集多径下接收机的复杂度,但是牺牲了一半的传输效率。
近几年,在密集多径信道下的非相干检测[45](NonCoherent Detection, NCD)得到了广泛关注,其代表技术是能量检测[67](Energy Detector,ED)。能量检测具有许多优势,例如无需进行信道估计,避免Rake接收结构,显著降低了对通信系统同步的要求等。这些优点为进一步降低无线通信系统复杂性以及为密集多径大带宽通信技术的发展提供了可行方案。然而,现有的非相干能量检测技术受到噪声和环境影响较为严重,其检测性能有待进一步提高。
信号稀疏表示理论由于其独特的魅力成为近20年来信号处理界一个非常引人关注的研究热点[8]。信号稀疏表示可以使得信号获得更为简洁的表达方式,从而使信号中所蕴含的信息更容易地表现出来,更方便进一步对信号进行加工处理[9]。本文针对现有能量检测的特征,提出一种基于稀疏信号处理的信号检测方案,用以提高非相干检测机制的性能。本文首先介绍了稀疏表示的原理,随后给出基于稀疏表示的稀疏信号分解、主成分分析及特征信号提取,最后利用假设检验方法对信号进行最终判决。为验证所提方案的可行性及有效性,本文通过仿真实验对比了传统方案与所提的方法,结果表明本文所提方案的检测能力更优秀。
1稀疏表示
稀疏表示[10]是指在某种变换或冗余完备字典上用尽可能少的测量值来表征原始信号。假设一个超完备冗余字典为D=[d1,…,dn],输入信号集合为y∈Rm,这个输入信号可以被重新表示为D与稀疏系数矩阵x=[x1,…,xn]T的一种稀疏线性组合,表达式为

这里,x即为输入信号y的稀疏表示系数。
稀疏表示的问题在于寻找n×1个最少非零系数x来表示y。这个问题常常使用求解一个优化问题,即0范数问题:
minx0s.t.y=Dx(2)
其中,0代表0范式,它的作用在于标记非零项个数。
更进一步,这个优化问题还可以等价于一个在1范式情况下的凸优化问题,模型如下:
minx1s.t.y=Dx(3)
其中,1代表1范式。
有许多算法可以求解这个优化问题,例如梯度投影算法[11]、贪婪算法[12]等。这里,本文使用的求解算法为正交匹配追踪(Orthogonal Match Pursuit,OMP)算法[13]。
2稀疏信号处理
根据稀疏表示原理,将原始脉冲信号在超完备字典下进行稀疏分解。在这一过程中,选择合适的超完备字典是非常重要的过程,因为这一过程不仅影响信号稀疏表示的稀疏性,还影响有用信号特征的选择。针对密集多径的信号特点,标准的多分辨字典是一种较为有效的选择,例如基于小波理论的字典。这些字典已经在已有的文献中用来处理自然场景图像,并且有较好的表现[14]。由小波函数ψ(t)及其扩展函数φ(t)经过平移伸缩以及尺度缩放,最终形成小波冗余字典:
ψj,k(t)=2-j/2ψ(2-jt-k)
φj,k(t)=2-j/2φ(2-jt-k) (4)
这里使用Symletes小波字典作为过完备冗余字典[15]。
依据公式(1)和(3),并且基于选定的过完备冗余字典,可以获取稀疏表示系数来重新表示原始的接收信号,也就是说,利用OMP算法和小波字典,接收信号可以被分解为稀疏系数。在这一过程中,原始的接收信号被转换为稀疏分解系数,而这些系数保留了原始信号特征成为进一步处理的对象。
通常,字典包含的原子数目大于接收信号数目,为了避免高维系数集的出现,有必要利用特征提取进行降维。本文使用主成分分析算法进行降维。
假设输入的稀疏系数为p=[p1,...,pn],想转换这些系数到一个更低的维度向量pV=[p1,...,pv],这一问题可以被表示为:
pV=E(p-μp)(5)
其中,pV是主成分分析系数,它可以以一种低维形式表示原始的稀疏系数向量。E包含协方差矩阵p中v个最大的特征值所对应的向量,而μp表示样本均值。
随后,利用这些经过稀疏表示以及主成分分析的系数集合,提取三个量化特征用以区分信号的不同特征,第一个特征为能量集中度:
![UY]2V~Y%I@LME60RU~NJCMO.png UY]2V~Y%I@LME60RU~NJCMO.png](http://files.chinaaet.com/images/2017/03/13/6362503801801760781652610.png)
3基于假设检验的信号检测
二元假设检验是信号检测中常用的策略,本文根据信号统计特性构建相对应的假设检验形式。二元假设检验是通过测量一组给定的假设状态来判定是否为所需信号:
Ho: 零假设
H1: 其他
存在两种类型的错误:虚假警报PFA(当H1被确定,但真实值为Ho时)以及漏检(当Ho被确定,但真实值为H1时),这里常用检测概率PD表示漏检的补集。
对于虚假警报PFA和检测概率PD,可以利用Neyman-Pearson定理[16]获取。当信号被接收者获取后,通过一些处理,其统计信号可以表示为:
f(τ)=(τ)+σ2(10)
其中,σ2是噪声方差。
这种情况下,假设f(τ)是服从高斯分布的统计特征,参考特征为f′(τ),从而得:
H0:f(τ)-f′(τ)=σ2
H1:f(τ)-f′(τ)=S+σ2 (11)
其中,S是区分与σ2的变量。
然后根据变量的统计特性分析和相应的统计信号检测,可以计算出目标特征的概率密度函数。通过预先设置虚警概率,可以计算获得检测概率和实际的虚警概率。这种条件下概率密度函数为:

其中ξ表示为PFA的阈值。
根据NeymanPearson定理,计算实际的虚警概率和检测概率分别为:

4数值仿真
在低复杂度非相干检测框架内,需要将信号调制方式考虑在内。由于非相干检测中不对信道冲激响应进行估计,相位调制方式将不适用,因而不采用移相键控(PSK)等相位调制。本文采用调时脉冲位置调制(THPPM),调制通过跳时机制实现时间多址接入,其调制信号可表示为:
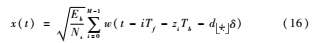
其中Tb表示单比特持续时间,Tf为帧时间长度,zi 为伪随机调时序列,δ为符号中比特间隔。
本文仿真采用IEEE 802.15.3a Task Group (TG)规定的SV多径信道模型。图1所示为典型视距传输距离为1~4 m通信场景下密集多径信道冲激响应。

图2表示在假设检验情况下稀疏信号处理过程,H0下仅包含加性白噪声,而H1下同时包含噪声和多径接收信号。从图中可以看出,两类信号在实域采集后的原始信号非常接近,而经过稀疏表示处理之后特征信息已经表现出来,但是特征空间相对较大,经过主成分分析后(PCA),相关的参数空间明显变少,而且特征信息依旧保留。因此,通过稀疏信号处理可以表征出这两类信号的不同,从而为信号的检测提供了特征信息。
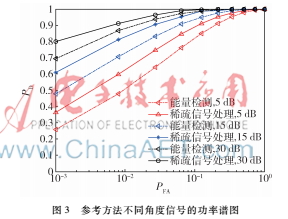
图3参考方法不同角度信号的功率谱图图3表示在经过假设检验后,本文所提方法与传统的能量检测方法性能相对比。实验分别从信噪比(SNR)为5 dB、15 dB、30 dB由低到高开展。从图中可以清楚地看到,随着信噪比的升高,两种方案的检测性能也有所提升,而且,在对虚警概率PFA的限制条件逐步放宽的前提下,检测性能PD逐渐趋近于1,这也是NP检测的特点所在,即在给定虚警概率的条件下,检测概率达到最好。从图中可以看出,无论是在哪种信噪比条件下,所提的基于稀疏信号处理的信号检测方法都比传统的能量检测方法性能优秀,这也说明了本文所提方法的有效性。
5结论
本文对密集多径信道下非相干信号检测方法进行了研究,为进一步提高非相干信号检测的性能,提出了一种基于稀疏表示的稀疏信号处理方案。本文构建了以稀疏表示为基础的特征信号,将假设检测方案作为最终的信号检测判决。仿真表明所提出的方法具有可行性,其检测性能要优于传统的能量检测方案。
参考文献
[1] Yang Liuqing, GIANNAKIS G B. Ultrawideband communications: an idea whose time has come [J]. IEEE Signal Processing Magazine, 2004, 21(6): 26-54.
[2] CASSIOLI D, WIN M Z, VATALARO F, et al. Low complexity rake receivers in ultrawideband channels [J]. IEEE Transactions on Wireless Communications,2007,6(4): 1265-1275.
[3] FRANZ S, MITRA U. Generalized UWB transmitted reference systems [J]. IEEE Journal on Selected Areas in Communications, 2006, 24(4): 780-786.
[4] GERALD J B, FERNANDES J R, CAEIRO P. Ultrawideband noncoherent transceivers[R]. Research Report, INESCID, Lisboa, 2010.
[5] BENAMOR I, TALL N, DEHAESE N, et al. A fully differential 7.28.5 GHz LNA for a self synchronized and dutycycled UWB OOK receiver[C]. 2015 IEEE International Conference on Ubiquitous Wireless Broadband (ICUWB), IEEE, 2015: 1-5.
[6] 陈长兴, 符辉, 牛德智,等. 基于双门限能量检测的协作频谱感知算法[J]. 系统工程与电子技术, 2013, 35(8):1742-1746.
[7] 张学军, 严金童, 田峰,等. 基于差分能量检测的双门限协作频谱感知算法[J]. 仪器仪表学报, 2014, 35(6):1325-1330.
[8] 张凤. 稀疏表示理论的研究及其在图像去噪中的应用[D]. 西安:西安电子科技大学, 2014.
[9] 崔嵩. 基于稀疏信号的学习字典算法及其应用[D]. 北京:北京工业大学, 2014.
[10] GUHA T, WARD R. Learning sparse representations for human action recognition [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(8): 1576-1588.
[11] FIGUEIREDO M A T, NOWAK R D, WRIGHT S J. Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems [J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 586-597.
[12] MALLAT S, Zhang Zhifeng. Matching pursuits with timefrequency dictionaries [J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415.
[13] TROPP J, GILBERT A. Signal recovery from random measurements via orthogonal matching pursuit [J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666.
[14] STARCK J L, ELAD M, DONOHO D L. Image decomposition via the combination of sparse representations and a variational approach [J]. IEEE Transactions on Image Processing, 2005, 14(10): 1570-1582.
[15] CHEN S S, DONOHO D, SAUNDERS M. Atomic decomposition by basis pursuit [J]. Society for Industrial and Applied Mathematics Review, 1998, 20(1): 33-61.
[16] KAY S M. Fundamentals of Statistical Signal Processing: Detection Theory Volume Ⅱ[M]. Prentice Hall, 2011.

