MIMO和OFDM技术结合能有效提高系统频谱效率并克服无线信道中严重的频率选择性衰落，是下一代无线通信的关键技术[1]。在MIMO-OFDM系统中，有最优检测性能的极大似然检测算法ML(Maximum Likelihood)及球译码算法[2]复杂度高。基于迫零ZF(Zero Forcing)和最小均方误差MMSE(Minimum Mean Square Error)的线性信号检测算法复杂度低，但当信道条件较差时，将产生噪声放大效果。目前针对MIMO系统，采用格点减少算法[3-4]对信道矩阵做预处理，算法复杂度低且能有效提高检测性能[5-7]。但在MIMO-OFDM系统中，信道矩阵变化快，这将产生大量列交换迭代。本文通过改进LLL算法并与排序的QR分解结合，先对信道矩阵做排序的QR分解得到上三角矩阵R,其对角线元素的模具有较好的升序排列，再对R进行LLL算法处理，处理中不再进行列交换运算，从而省去LLL算法中的迭代，大大减少了计算复杂度。

1 系统模型

　　考虑MIMO-OFDM系统发送端和接收端分别有NT和NR(NR≥NT)个天线。假设传播信道为频率选择性信道，每个发射天线和接收天线间的信道衰落独立。接收端在多路频域信号流的同一子载波上采用MIMO接收算法检测。系统模型可表示为：

　　yi=Hisi+zi (1)

　　其中，si代表第i个子载波上的NT×1发送信号矢量，E{(si)(si)H}=I；yi表示第i个子载波上的NR×1接收信号矢量；NR×1维矢量zi代表各维独立的高斯白噪声，E{(zi)(zi)H}=z2I;Hi代表NR×NT信道矩阵，其元素为单位方差互不相关的复高斯衰落增益，假设Hi帧内保持不变，帧间独立变化。

　　若分别处理式(1)中实部和虚部，省略上标，信道模型可转化为：

　　y=Hs+z (2)

　　其中实值矩阵H为：

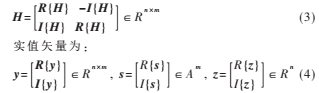
　　R{·}和I{·}代表取实部和取虚部，n=2NR和m=2NT代表维数, A代表有限实数集。

2 格点减少算法

　　在实数信道模型中，假设发送信号矢量的各维为整数，则所有可能的无噪声接收信号Hs可视为一个格点集，该集以H的列矢量为基矢量，每个格点都是这些基矢量的线性组合。同时该格点集也可用矩阵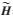=HT的列矢量为基矢量表示，T为幺模矩阵。采用QR分解，H=QR，系统方程(2)可写为:

　　y=QRs+z (5)

　　矩阵条件数定义为k(H)=max/min=‖H‖2‖H-1‖2≥1，

max、min为H的最大和最小奇异值。通常信道矩阵条件数越大，噪声放大越大，线性检测的判决域也越狭小;相反，对正交矩阵k(H)=1，将无噪声放大，判决域也最大。式(5)中， Q是酉矩阵， ‖QR‖2=‖RQ‖2=‖R‖2， k(H)=‖QR‖2‖R-1Q‖2=‖R‖2‖R-1‖2=k(R)，所以H和R有相同条件数。格点减少算法的目标是找到一个等效的系统方程，其信道矩阵的条件数小于R的条件数。

　　基于R矩阵的LLL算法便是一种有效的格点减少算法。LLL减少的两个条件为：

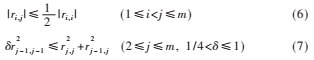
　　其中ri,j为R矩阵第i行j列元素，取值0.75具有最佳约减效果[2]。式(6)使基矢量的模减小，矩阵条件数减小。式(7)将新基矢量与原基矢量比较，进一步减小模，使各基矢量更接近正交。通过LLL算法处理得到约减的矩阵RLLL，此时系统方程(5)可写为：

　　新系统方程将被认为是条件良好的，对其线性检测时，噪声放大减小，判决域增大。

3 改进的格点减少算法

　　3.1 约减LLL算法分析

　　LLL算法复杂度主要取决于为满足式(7)而进行的列交换迭代次数。最坏时，随天线数增加，复杂度是无界的[2]。参考文献[5]指出，在4×4天线配置下，传统LLL算法平均列交换次数为13.2次，若FFT长度为64，则每帧MIMO-OFDM信号将产生844.8=64×13.2次列交换。

　　信道矩阵H的元素都是独立的高斯变量，经过式(6)处理后各列矢量间高度相关的概率较小，因此当约减的LLL算法只采用式(6)进行矢量模减小，然后对新的信道矩阵采用线性检测时,将得到一个较大的判决域，而噪声放大也不是很大,通常能得到较好的误码率曲线。且因省去列交换的迭代，算法复杂度大大减小。

　　3.2 约减LLL算法和排序QR分解结合检测

　　当信道矩阵的维数较小时，矩阵元素的初始值易使式(6)恒成立，采用约减的LLL算法将使矩阵得不到约减。为使约减性能达到LLL算法，并避免其算法的大量迭代，在约减的LLL算法前，先对信道矩阵进行wubben排序QR分解[8]。它在QR分解过程中排序，使R矩阵的对角线元素的模|ri,j|尽可能从小到大排列。这样，R矩阵中大部分元素满足式(7),此时采用约减的LLL算法将达到LLL算法的性能。参考文献[8]指出排序的QR分解的计算开销和未排序的QR分解相比几乎可忽略。因此在4×4天线配置下，排序的QR分解与约减的LLL算法结合，其计算复杂度与LLL算法相比，每帧MIMO-OFDM信号节约844.8次列交换。

　　H矩阵经过排序QR分解，将满足如下表达式：

4 性能仿真分析

　　在2×2和4×4天线配置下，本节给出两种检测方案与ZF、MMSE、ML及LLL算法的性能比较，如图1、2所示。OFDM信号的FFT长度为64，循环前缀为16，调制方式为16-QAM，信道编码为卷积码。

　　从图1和图2知，天线配置为2×2时，约减的LLL算法(SLR-MMSE)相对线性检测，性能提升较小。由于基矢量较少被约减，它与排序QR分解结合检测(SortedSLR-MMSE)的性能相对于LR-MMSE算法,在BER=10-3时，信噪比损失约0.2 dB。约减LLL算法的性能提升随天线数增加而增加，在4×4天线配置时，约减LLL算法与排序QR分解结合后,其性能优于LLL-MMSE算法，在BER=10-3时,信噪比节省约0.2 dB,且复杂度降低更多。 本文提出一种约减LLL算法与排序QR分解结合检测，其省去了LLL算法的列交换迭代，在保障误码性能的情况下，减少了计算复杂度，其性能提升随天线数增加而增加。该算法未采用最优的QR排序，因此采用最优排序分解以及与串行干扰相消、球形译码等非线性检测结合亦可进一步研究。

　　参考文献

　　[1] 宁宁. 基于MIMO-OFDM系统的自适应算法研究[J].微型机与应用, 2011,30(2):62-64.

　　[2] 唐元元,张德民,刘哲哲,等.TD-LTE系统中软输出球形译码检测算法研究[J]. 电子技术应用, 2012,38(11):55-58.

　　[3] YAO H， WORNELL G W. Lattice-reduction-aided detec-tors for MIMO communication systems[C]. IEEE GlobalTelecommunications Conference,2002(1):424-428.

　　[4] LENSTRA A K, LENSTRA H W, LOVSZ L. Factoringpolynomials with rational coefficients[J]. Mathematische An-nalen, 1982,261(4):515-534.

　　[5] WBBEN D, BHNKE R, KHN V, et al. MMSE-basedlattice-reduction for near-ML detection of MIMO systems[C].ITG Workshop on Smart Antennas,2004:106-113.

　　[6] GAN Y H, MOW W H. Multiple-input multiple-outputsignal detectors based on relaxed lattice reduction[P].UnitedStates, Patent Application Publication,13/348,469.2012-1-11.

　　[7] WEN Q, ZHOU Q, ZHAO C, et al. Fixed-point realiza-tion of lattice-reduction aided MIMO receivers with com-plex K-best algorithm[C]. 2013 IEEE International Con-ference on Acoustics, Speech and Signal Processing,2013:5031-5035.

　　[8] WBBEN D, BHNKE R, KHN V, et al. MMSE exten-sion of V-BLAST based on sorted QR decomposition[C].2003 IEEE 58th Vehicular Technology Conference,2003(1):508-512.