文献标识码: A
文章编号: 0258-7998(2014)04-0103-03
随着计算机及数字信号处理技术的发展,全数字接收机[1]在卫星通信技术中得到了广泛应用。由于多普勒频移及移动终端与卫星之间长的传播时延,不可避免地存在采样时刻偏差,导致接收端数据样点并不一定在最佳采样点上,从而造成了误码。
然而在卫星通信系统中,信号调制载波频率存在较大偏移[2],这将对数据的正确解调产生严重的影响。为了解决这个问题,本文在Gardner改进算法E-Gardner(Evolved Gardner)[3]的基础上提出了一种用于数字通信接收端时钟误差检测模块的抗载波偏差算法AC-Gardner(Anti Carrier Gardner)。该算法可以在载波偏差存在的情况下工作,并表现出接近无载波偏差时的性能,提高了原算法的可靠性和准确度。
本文简单介绍了基于全数字接收的改进定时同步环路模型,并对所提出的AC-Gardner算法作了详细的原理描述和数学证明,对AC-Gardner算法进行了仿真,其结果与E-Gardner算法在S曲线斜率、误码率等性能方面做了比较。
1 AC-Gardner误差检测算法

图1为改进的定时同步环路模型,主要由插值滤波器、时钟误差检测器TED(Timing Error Detector)、环路滤波器及定时控制器四部分组成。该改进模型与传统定时同步环路[4]的区别在于TED模块中不仅采用E-Gardner算法,而且还增加了载波偏差估计与补偿部分。该模块既能实现无载波偏差信号的定时误差检测,也能对含载波偏差的基带信号先进行定时误差检测,再进行载波频偏与相偏估计,最后与数字下变频后的基带信号进行复数乘法运算得到校正信号。
根据该定时环路模型,接收的信号经下变频后得到:
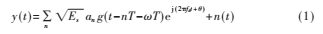
其中,an为正交QPSK符号的发送序列,an=exp(j·in),in=0,1,2,3,Es=1为符号能量,n为符号序列,T为码元宽度,为从发射机到接收机的归一化传播时延,g(t)为升余弦脉冲,fd为多普勒频移,收发载波固定相差,n(t)为加性复高斯白噪声。
对y(t)采样并使其进入定时同步环路得到的E-Gardner算法的表达式为:

当定时同步环路进入稳定状态后,对连续的QPSK信号经本地固定时钟采样及插值滤波器后,可以得到每个符号的最佳采样点。假设发送信号的幅度相同,且在传播过程中衰减一致,则接收信号最佳采样点的幅值大约相等。于是得到:
![PZY$K}B21[Y{BO7Y6`]B{XW.png PZY$K}B21[Y{BO7Y6`]B{XW.png](http://files.chinaaet.com/images/2017/01/23/6362079752277900005952989.png)
因此,多普勒频移fd对TED模块定时误差检测性能的影响不是线性的,而是周期性的,如图2所示。
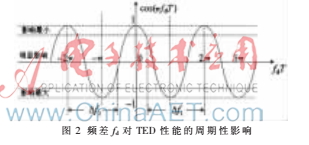
为了消除多普勒频移对TED模块性能的影响,必须将多普勒频率搬移到其对频偏几乎无影响的区间,即只需将多普勒频移fd搬移至2/T的整数倍即可,所以必须计算出搬移频率的大小。
由于余弦函数![RP}_KKW6$CE%%I_Z1@]W}IY.jpg RP}_KKW6$CE%%I_Z1@]W}IY.jpg](http://files.chinaaet.com/images/2017/01/23/6362079755504000005174498.jpg) 为周期,于是整个区间上的搬移频率
为周期,于是整个区间上的搬移频率![YFJW{Q)1I][U%J5_)D6TV[D.jpg YFJW{Q)1I][U%J5_)D6TV[D.jpg](http://files.chinaaet.com/images/2017/01/23/6362079759304700001757205.jpg) 为:
为:
![CAW0K36(UE7S5X495~P7`]H.png CAW0K36(UE7S5X495~P7`]H.png](http://files.chinaaet.com/images/2017/01/23/6362079754395100009525693.png)
因而,将计算的搬移频率与数字下变频后的基带信号进行复数乘法运算,最终得到矫正的基带信号。
2 仿真结果及性能分析
信道环境:用Matlab在基于乡村阴影环境的Corazza信道模型下对AC-Gardner算法的性能进行仿真,仿真参数配置表如表1所示。

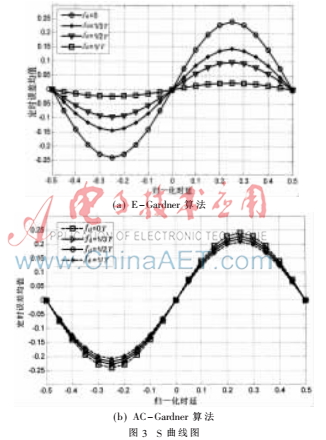
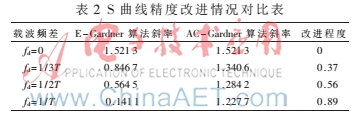
对于一个定时误差检测算法,S曲线可以直接反映算法的性能好坏。通常,S曲线越平滑且越陡峭,对应的算法性能就越好。所以为了进一步验证AC-Gardner算法的性能,需进行开环仿真。图3为E-Gardner算法和AC-Gardner算法存在载波偏差时的S曲线图。按照以S曲线在零点处的斜率代表精确度这个标准验证AC-Gardner算法的精度性能,由前面推导得知,载波频差fd对TED性能呈周期性影响。所以为了简便起见,只需统计两种算法在载波频差fd∈[0,1/T]的精确度,表2为其S曲线精度改进情况对比表。从该表中知道,存在载波偏差时,与E-Gardner算法相比,AC-Gardner算法精度性能约提升37%~89%左右。
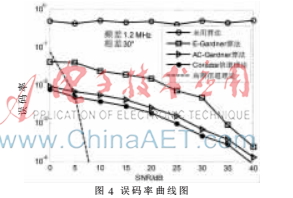
AC-Gardner算法性能可用接收端QPSK信号的误码率来分析,从图4仿真结果可知,当载波频偏fd=1.2 MHz时,随着信噪比的增加,尽管误码率曲线是逼近理想高斯白噪声信道的,但由于多径衰落及阴影效应,信号有很强的衰落,存在较大的误码率。通过对比发现, AC-Gardner算法误码率曲线很贴近Corazza信道理论曲线。当信噪比为20 dB时,E-Gardner算法的误码率约为1.8×10-2,AC-Gardner算法误码率约为2.5×10-3,经计算后者性能提升约8.57 dB。而且,在信噪比[0,40] dB范围内,AC-Gardner算法的平均增益约为8.46 dB。因此,当信号中存在载波频差和相差时, AC-Gardner算法的校正性能较好。
本文提出了一种适用于卫星通信数字接收端TED模块的AC-Gardner算法,并给出了该算法的数学推导过程,同时在Corazza卫星信道环境下从频差估计范围、S曲线斜率、误码率等三方面对其正确性进行了验证。仿真结果表明,AC-Gardner算法不仅增强了Gardner及其改进算法对抗载波偏差的性能,同时也继承了Gardner算法实现简单、硬件消耗较小、对相位偏差不敏感的特点。所以,AC-Gardner算法能很好地克服卫星通信中存在的多普勒偏移及加速度等难点,在全数字解调尤其是卫星移动通信系统中有着较高的应用价值。
参考文献
[1] MARAL G, BOUSQUET M. Satellite communications sys-tems: systems, techniques and technology[M].3rd ed.[S.l.]:Wiley, 2011.
[2] 张公礼.全数字接收机理论及技术[M]. 北京:科学出版社, 2005.
[3] LIM D. A modified Gardner detector for symbol timing re-covery of M-PSK signals [J]. IEEE Trans. On Communi-cations, 2004,52(10):1643-1647.
[4] Chen Yang, Wang Yongqu. The design of a symbol timingsynchronization system for all digital receiver[J]. Microcom-puter Information, 2010(23):071.
[5] 刘强, 陈西宏, 周进. 对流层散射多径信道估计性能分析[J]. 电子技术应用, 2011,37(3):94-97.
[6] 付永明,朱江,琚瑛珏. Gardner 定时同步环路参数设计及性能分析[J].通信学报, 2012,33(6):191-198.
[7] 唐筠. 同步头辅助的 MPSK 信号高精度频偏估计[J].微型机与应用, 2011,30(20):65-67.

