张堂凯,罗杰,李龙俊
(南京邮电大学 自动化学院,江苏 南京 210023)
摘要:智能清洁机器人全局路径规划中,利用栅格法对清洁机器人的工作环境进行建模。分别介绍了K-Means聚类算法和支持向量机(SVM)算法,使用K-Means聚类算法与支持向量机(SVM)相结合的方法,以不同的约束条件进行聚类,在含有复杂障碍物的栅格地图时能有效减少分区,利用蚁群算法对分区后的栅格地图路径规划仿真,有效地提高了蚁群算法在栅格地图路径规划中的整体效率。
关键词:栅格地图;K-Means聚类;支持向量机(SVM);蚁群算法
0引言
目前市场上的智能清洁机器人在路径规划上大多数采用随机遍历的策略,清扫的全遍历差,耗时长。路径规划是智能清洁机器人的基础问题,对于规划路径的优化主要在于提高清扫覆盖率,降低重复率。
蚁群算法是智能理论研究领域的一种主要算法,可以用于大部分需要优化的应用领域,其中潜力比较大的领域主要有:模式识别、信号处理、电力控制以及移动机器人路径规划等。曾碧[1]等人将蚁群算法与一种概率路线图相结合来规划机器人路径,该方法可以减少蚁群算法在进行大规模路径规划的时间。张赤斌[2]等人将Boustrophedon单元分解法与蚁群算法相结合,采用局部区域遍历与全局运动相结合的完全遍历路径规划方法,在降低算法复杂性的同时又加快了算法的收敛速度。但是蚁群算法还具有容易收敛到局部最优解和解决大规模优化问题时收敛速度过慢的缺点。这些缺点影响了蚁群算法在路径规划方面的使用。
针对路径优化算法在解决完全遍历路径规划效率低下的问题,本文使用K-Means聚类算法与支持向量机(Support Vector Machine,SVM)相结合的方法,以不同的约束条件进行聚类,使得栅格地图被纵向地分割成几个区域,然后再利用蚁群算法对分割完成的栅格区域进行路径寻优,使得蚁群算法总体效率大幅增加,有效地减少了算法的收敛时间,取得了很好的路径规划效果。
1地图建模

栅格法(Grid)以地图的二维环境模型作为基础,将地图分成若干个栅格,每个栅格记录周围环境的信息[3]。
以环境地图二维栅格图的左下角为原点,Y轴竖直向上,X轴水平向右,单元栅格的边长为1。MATLAB基于栅格法的环境建模效果图如图1所示。
本文使用MATLAB平台对栅格地图的优化进行仿真实验。使用直角坐标系法对栅格地图进行标识,环境中一共有6个障碍物,其中1个凹形障碍物,5个矩形障碍物。
2基于K-Means的栅格障碍物聚类
K-Means聚类算法由MACQUEEN J B[4]在1967年提出,K-means算法的基本思想是:从给定的n数据样本的集合中任取k个数据样本作为初始的聚类中心,再根据相似性度量函数计算其他未被选取的数据样本与各个聚类中心的相似性,并根据该相似度,将该数据样本划分到与它相似性最高的聚类中心所在的簇类中,根据簇类中样本的平均值更新聚类中心,直到簇类内误差平方和最小[5]。
2.1聚类步骤
K-Means聚类算法对栅格地图中的障碍物进行聚类,主要步骤如下:
(1)将障碍物栅格坐标输入样本集: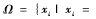
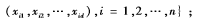
初始化最大簇类个数为K,最大迭代次数为Tmax,系统允许最大误差为εmax;
(2)从Ω中随机选取K个栅格坐标作为初始簇类中心,记为:
(3)定义dis(xi,cj)为任意点xi和任意点xj之间的欧几里得距离,公式如下:
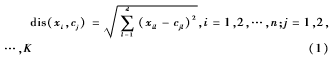
计算点xi与点xj之间的欧几里得距离,将样本点xi按公式(2)计算,其中sij属于集合C。
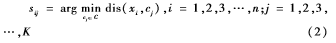
将样本点xi分配到离它最近的簇类中。
(4)按照公式(3)更新中心。其中cj为同一个簇类的中心点,N(φj)为簇类φj中数据样本的个数,xi=(xi1,xi2,…,xid)。
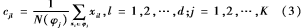
(5)按照公式(4)计算每个簇类内的评价函数SSE。
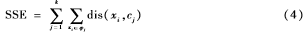
(6)如果|SSET-SSET-1<εmax|或者T=Tmax,循环结束并输出结果;否则令T=T+1跳转步骤(2)。
2.2聚类仿真实验
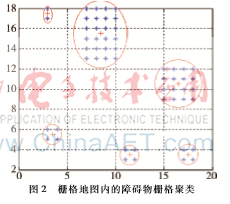
将障碍物栅格点xi和点xj的欧几里得距离带入算法进行仿真,使代表障碍物的栅格聚集到一起,得到图2所示的聚类效果图,其中“+”为簇类中心。
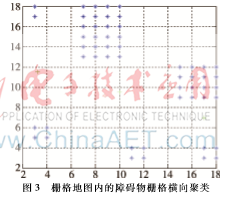
再将栅格点xi和点xj横坐标欧几里得距离带入算法进行仿真,使得栅格地图中代表障碍物的栅格横向聚成3类,得到图3所示的聚类效果图,图中浅色的“+”为新的簇类中心,这为下一步的分区做准备。
3基于SVM的栅格地图分区
SVM算法通过寻求结构化风险的最小,来增大算法学习机的泛化能力,在最小化经验风险的同时获得最优的置信区间[6]。使用SVM算法处理数据样本,即使样本数量较少也能获得比较好的统计规律。SVM算法是统计学习、最优化方法与核函数方法的结合[7]。
SVM的基本思想如图4所示,实心圆圈和空心圆圈分别代表两种不同的数据样本,H为最优分类界面,H1和H2分别是数据样本类型的类界图4线性可分情况下的最优分类线面,两个类界面之间的距离叫分类间隔(margin),类界面与最优分类界面之间的距离叫界面间隔[8]。最优分类界面要求将两类数据样本分开的同时保证分类间隔最大。分类界面的数学表达式为:

将其归一化,使得对线性可分的数据样本(xi,yi),xi∈Rn,yi∈{1,-1},i=1,2,…,l,满足:
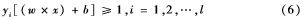
此时分类间隔等于2/w,要使间隔距离最大也就是要使得w2最小并符合式(6)的最优分界面。
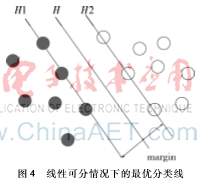
SVM要解决的数学问题可以理解为在满足式(7)条件下,求解式(8)的最小值。
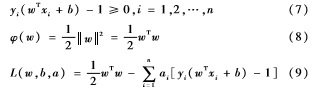
定义L(w,b,a)函数如式(9),系数ai≥0。这样就可以通过w和b求函数的最小值来求得φ(w)的最小值。
将式(7)作为约束条件,求最小值问题就可以转化为凸二次规划的对偶问题。
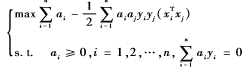
这是一个在不等式约束条件下求解二次函数解的问题,存在唯一最优解。不妨令a*i为最优解,则
 其中a*i的值不是零的数据样本就是支持向量。b*可由φ(w)=0解得,最后求得的最优分类函数为:
其中a*i的值不是零的数据样本就是支持向量。b*可由φ(w)=0解得,最后求得的最优分类函数为:
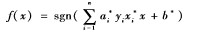
将第2节横向聚类得到的图3使用SVM分类算法对栅格进行分类,得到如图5和图6的结果,图中标出的栅格点为分类算法的支持向量,将支持向量的坐标和最优分类面在y=0、y=ymax的坐标都提取出来,用于栅格地图分区。
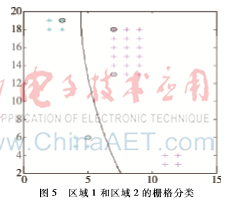
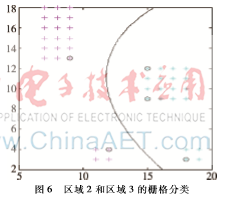
利用之前提取的支持向量的坐标、分类面和边界的坐标,结合第2节中的聚类结果,生成一个多边形。再计算出多边形的边y={1,2,3,…,ymax}时对应的x值,然后比较栅格中点与多边形边上点相同y值情况下,x值的大小关系,根据x值大小的不同可以将栅格地图划分为3类。
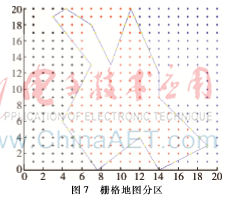
仿真实验如图7所示。相对于基于四叉树的栅格地图分区和基于Boustrophedon单元分解法的栅格地图分区,本文中基于K-Means和SVM的栅格地图分区数量更少,在解决栅格地图中含有大量障碍物栅格时也能取得较好的分区效果。
4蚁群算法以及仿真
蚁群能够协同完成很多复杂的任务,蚁群算法只是对蚁群觅食行为的抽象与优化。
蚁群算法:首先初始化参数,然后将m只蚂蚁随机地放置到n个城市中,同时更新禁忌表tabuk。开始时,每条路径上的信息素量相等,设(C为常数)τij(0)=C。蚂蚁根据启发式信息和每条路径上的信息素量选择它要去的下一地点[9]。蚂蚁k在t时刻从点i转移到点j的概率pkij(t)为:
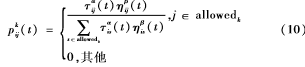
其中,allowedk={1,2,…,n}-tabuk是蚂蚁下一步可以选择去的点。禁忌表tabuk中存储了蚂蚁已经走过的点,当tabuk中存储点的数量等于n时,说明蚂蚁k本次循环结束。式(10)中通常取ηij=1lij,α为信息启发因子,即路径的相对重要性;β为期望启发因子,即启发因子的相对重要性。当一次循环完成后,根据式(11)更新路径上的信息素。
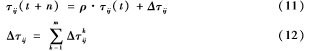
其中ρ为信息素残留系数,0<ρ<1,1-ρ为信息素挥发系数[9]。
根据信息素更新策略不同,给出了Δτkij的更新方法,在Ant Cycle模型中:
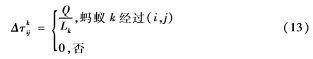
其中Q为信息素强度,为蚂蚁在一次循环中在走过的路径上释放的信息素总量,它影响算法的收敛速度,Lk为第k只蚂蚁单次循环中走过的路径长度的总和。
Ant Cycle模型使用的是全局信息,即所有蚂蚁完成一次遍历之后再对路径上残留的信息素进行调整。
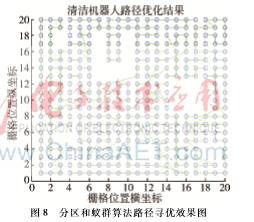
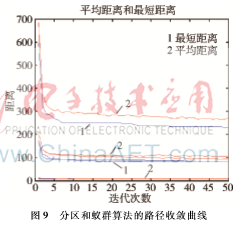
根据上面的分析,实验选取适当的参数,使用蚁群算法对第3节中已经分区完毕的栅格进行仿真实验。实验参数设置为ρ=0.15,ε=0.1,β=2.5,m=30,q0=0.85,NCmax=50。得到图8所示的实验效果图,图9为基于聚类分区和蚁群算法的清洁机器人路径收敛曲线。
5结论
本文提出了一种新的基于聚类分区和蚁群算法的清洁机器人路径规划方法。利用栅格法对清洁机器人的工作环境进行建模,使用K-Means聚类算法与支持向量机(SVM)相结合的方法对栅格进行分区,再利用蚁群算法对分割完成的栅格区域进行路径寻优。清洁机器人沿着优化路径完成对已知环境的全区域覆盖,仿真实验结果表明,本文提出的方法能够高效地实现清洁机器人全局路径规划。
参考文献
[1] 曾碧, 杨宜民. 动态环境下基于蚁群算法的实时路径规划方法[J]. 计算机应用研究, 2010, 27(3):860-863.
[2] 张赤斌,王兴松.基于蚁群算法的完全遍历路径规划研究[J].中国机械工程,2008,19(16):1945-1949.
[3] 田春颖,刘瑜,冯申坤.基于栅格地图的移动机器人完全遍历算法——矩形分解法[J].机械工程学报,2004,40(10):56-61.
[4] 李荟娆.K-means聚类方法的改进及其应用[D].哈尔滨:东北农业大学,2014.
[5] JAIN A K. Data clustering: 50 years beyond Kmeans[J]. Pattern Recognition Letters, 2010, 31(8): 651-666.
[6] 梁燕.SVM分类器的扩展及其应用研究[D].长沙:湖南大学,2008.
[7] 张学工. 关于统计学习理论与支持向量机[J]. 自动化学报, 2000, 26(1): 32-42.
[8] VAPNIK V N,VAPNIK V.Statistical learning theory[M]. New York: Wiley, 1998.
[9] 王越, 叶秋冬. 蚁群算法在求解最短路径问题上的改进策略[J]. 计算机工程与应用, 2012, 48(13): 35-38.

