薛志强，林金星
　　（南京邮电大学 自动化学院 ，江苏 南京 210023）

摘要：以高超声速飞行器纵向通道为研究对象，考虑飞行器控制系统中传感器–控制器以及控制器–执行器通道均存在数据丢失的问题，提出一种能有效处理丢包的预测控制方法。首先，对高超声速飞行器纵向通道非线性模型进行局部小扰动线性化，得到平衡点处线性化模型；接着，建立有数据丢失的系统动态模型，使用终端状态约束集和终端代价函数方法设计预测控制器并设计相关补偿策略，以实现高超声速飞行器输入指令的跟踪；最后，基于MATLAB和Truetime平台进行数值仿真。结果表明,所设计的预测控制器能保证系统在出现数据丢失时具有良好的跟踪性能和鲁棒性。
关键词：高超声速飞行器；数据丢失；预测控制；Truetime　　

0引言
　　高超声速飞行器是指飞行速度超过5马赫的飞行器，具有速度快、反应时间短、突防能力强等特点［1］，其也是一个强非线性多变量系统。同时，飞行器飞行时对空气动力学参数以及大气条件的变化非常敏感。目前，一些先进的控制策略被应用到高超声速飞行器控制，如:鲁棒控制［23］、自适应控制［45］和反步控制［6］等。这些控制方法主要从不同方面改进了系统鲁棒性能，但是这些方法在设计控制器时难以显示处理控制量和状态的约束，而在飞行器控制系统设计时需要考虑这些约束量。
　　预测控制因其能有效处理具有约束多变量系统的特点被广泛应用于工业工程中。近年来，运用预测控制设计高超声速飞行器控制系统已成为一个热点［711］。例如：参考文献［8］研究了高超声速飞行器巡航飞行时的鲁棒预测控制器，使其在模型参数发生变化时仍能保证飞行器稳定飞行；参考文献［9］针对给定飞行条件，首先对高超声速飞行器纵向通道非线性模型在平衡点附近进行线性化处理，然后针对该线性化模型设计了预测控制器；参考文献［10］将调度预测控制的思想应用于离线鲁棒预测控制, 设计了高超声速飞行器计算有效的调度离线预测控制器；参考文献［11］将模型预测控制方法应用于高超声速飞行器纵向通道的姿态控制中。
　　但是，上述文献都假设飞行器控制系统中传感器–控制器通道以及控制器–执行器通道数据是完整传输的。然而，由于实际系统中数据传输时不可避免地存在拥塞或数据碰撞、节点故障或连接中断等问题，使得飞行器系统中传感器–控制器以及控制器–执行器通道出现数据丢失现象，这将导致控制系统性能下降，严重可能出现系统失稳。因此，考虑具有数据丢失的控制系统设计已成为控制界的一个研究热点［1213］。参考文献［12］针对非线性系统模型研究了由系统控制器输出通道数据丢失导致的执行器故障问题；参考文献［13］研究了含有多概率时延和多个测量量丢失的不确定离散模糊系统的鲁棒H∞控制问题。
　　针对上述问题，本文研究高超声速飞行器传感器控制器以及控制器执行器通道均存在数据丢失时的预测控制器设计。首先解耦飞行器非线性数学模型得到纵向部分，再将此模型线性化，接着考虑具有数据丢失的系统动态并设计其预测控制器，最后通过Truetime的数字仿真来验证控制器的有效性。
1高超声速飞行器动态模型
　　1.1非线性动态模型
　　高超声速飞行器全状态非线性运动方程存在强烈的三通道(即滚转通道、俯仰通道、偏航通道)耦合特性。在假设飞行状态满足水平无侧滑条件时，可将原系统进行三通道解耦，把高超声速飞行器的运动分为纵向和横向两部分。同参考文献［14］，本文主要针对高超声速飞行器纵向通道(即俯仰通道)进行研究。一种典型的简化纵向通道运动方程组如下：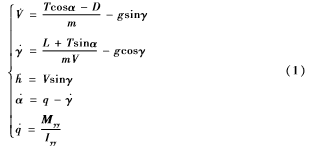

　　其中V表示飞行速度，γ表示航迹倾斜角，h表示飞行高度，α表示飞行攻角，q表示俯仰角速率，g表示重力常数，T表示发动机推力，D表示阻力，L表示升力，Myy表示俯仰力矩，Iyy表示转动惯量。气动力(D，L)和力矩Myy表示为：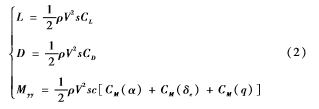

　　气动导数为：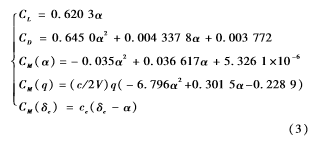

　　式中，CL表示升力系数，CD表示阻力系数，CM(α)、CM(δe)、CM(q)分别表示与攻角、舵偏角以及俯仰角速率有关的力矩系数，c表示参考长度，δe表示舵偏角，ce表示力矩常系数，ρ表示空气密度，s表示参考面积。
　　发动机的推力计算公式为：

　　其中CT表示推力系数，且CT=0.025 76β，β>1
　　0.002 4+0.003 36β，β<1。
　　动力系统动态方程采用二阶系统模型：

　　式中β为发动机节流阀调定值,βc为常量油门开度。
1.2模型线性化
　　在预测控制算法中，若预测模型为一非线性模型，则在滚动优化中，每一时刻需要在线求解一个非凸优化问题，使得获取全局最优解变得相当困难，减弱了其实用价值。本文根据高超声速飞行器特定的巡航条件(飞行速度V0和飞行高度h0)，首先采用MATLAB的findop函数计算高超声速飞行器平衡状态x0=［V0,γ0,h0,α0,q0］T，接着在该平衡点附近利用局部小扰动线性化方法进行模型线性化［15］，然后以一定采样间隔进行离散化，最后获得5阶离线线性模型：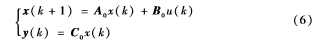

　　式中，状态x=［V,γ,h,α,q］T；输出y=［V,h］T，控制输入u=［β,βc］，A0、B0、C0分别为相对应的系数矩阵。
2考虑数据丢失的高超声速飞行器预测控制器设计
　　2.1控制系统结构
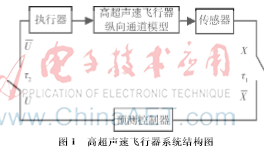
　　本文高超声速飞行器纵向通道系统结构如图1所示，在传感器和控制器之间以及控制器和执行器之间均存在数据通道。由于存在数据丢失(由开关τ表示)现象，可能出现控制器没有获取传感器采集的信息(由状态X表示)以及执行器没有得到控制器计算的控制量(由状态U表示)等情况。

2.2考虑数据丢失的系统动态模型
　　现有文献［16］对丢包描述一般是引入Bernoulli或Markovian过程来表示网络中数据的随机丢失,随机变量γ(k)表征系统传输的不完整数据包的到达状态，并且满足在0与1间取值(γ(k)=1表示k时刻无丢包，γ(k)=0表示k时刻有丢包)，从而建立数据丢失概率与系统性能之间的关系。本文为了满足数据丢包过程的一般性，不要求其满足某种特定的概率分布，建立最大连续数据丢失数与系统性能之间的关系。所以考虑图2所示的数据丢失模型［17-18］，假设只有d0,d1,…,di,di+1,di+2,…时刻的数据能够由传感器成功传送至控制器；同时只有h0,h1,…,hi,hi+1,hi+2,…时刻的数据能够由控制器成功传送至执行器。

　　根据图2，在时间［di,hi+1)内，如果di时刻系统状态x(di)求出的最优控制序列u(k|di)没有到达执行器，则执行器选用di－1时刻由控制器解出的控制量u(k|di－1)；如果在di时刻最优预测控制序列达到执行器，则执行器选用当前控制量u(k|di)。综上所述，在时间［di,hi+1)内可以建立如下飞行器控制系统模型：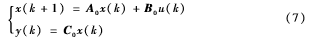

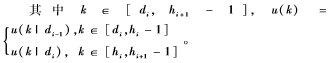
2.3预测控制器设计
　　本文使用终端状态约束集和终端代价函数方法设计约束预测控制器［18］。这种方法在保证闭环系统稳定性的同时，仅将系统终端状态驱动到一个不变集里，摆脱了终端等式这种强约束条件。但是，传感器–控制器通道数据的丢失导致系统状态间断到达控制器，这样使得控制器只在成功接收到数据的时刻计算预测控制量并将其传送到执行器，而在其他时刻不进行控制量的计算。下面给出控制器在成功接收到传感器数据时刻预测控制量的具体算法。
　　首先考虑如下优化问题：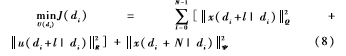

　　s.t.
　　x(di+l+1|di)=Ax(di+l|di)+Bu(di+l|di)
　　u(di+l|di)≤umax,u(di+l|di)∈U(di)
　　x(di+N|di)∈XT
　　其中，u(di+N|di)表示在di时刻飞行器系统状态x(di)在d+i时刻控制器计算出控制输入的预测值，也是上述优化问题的优化变量；x(di+i|di)表示在di时刻飞行器系统状态x(di)在d+i时刻的系统状态的预估值。此外，Q>0和R>0分别是状态和输入的加权矩阵，N表示控制时域和预测时域，正定对称矩阵Ψ是终端加权矩阵，满足下列条件：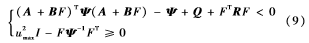

　　要使公式(9)成立，通过Schur变化得到如下优化问题：
　　minM>0,W-logdet(M)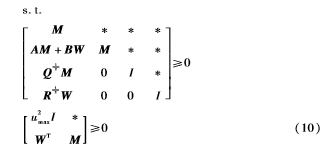

　　从而可以得到终端加权矩阵Ψ=M－1和局部镇定控制律F=WM－1，以及终端状态约束集XT={x:xTΨx≤1,Ψ=M－1}。
　　当离线求解出局部镇定控制率F、终端状态约束集XT和终端加权矩阵Ψ后，飞行器系统实时控制只需要求解优化问题（8）即可。根据预测控制基本原理，N步的状态预测值可由下面的公式导出：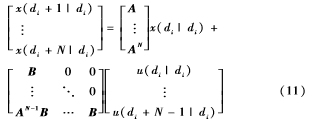

　　且可以等价为: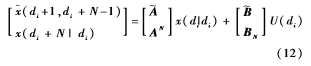

　　因此，优化问题中的性能指标可以转化为如下形式：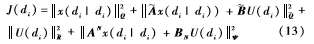

　　其中，与分别是对角元素为Q与R的对角矩阵。所以，针对具有有界丢包的飞行器控制系统（如式(5)所示），在线优化问题可由下面的线性不等式代替：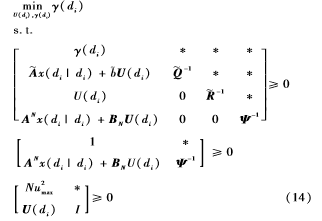

　　当di时刻优化问题（式(14)）存在最优解时，控制输入可以表示为：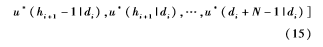

　　控制系统补偿预测控制的具体设计步骤如下。
　　（1）通过求解LMI优化问题（式(10)）得到局部镇定控制率F、终端状态约束集XT和终端加权矩阵Ψ。
　　（2）当初始成功传输时刻d0满足d0　　（3）在di采样时刻，根据已知状态信息x(di)=x(di|di)，在线求解优化问题（式(14)），得到最优控制序列U*(di)。在时间［di,hi+1)内，一开始执行器没有接收到U*(di)，则其选取di－1时刻解出的最优控制序列U*(di－1)中的预测控制量U*(hi+j|di－1),j=di－hi,di－hi+1,…－1，并将其作用于执行器；当执行器在hi时刻接收到序列U*(di)时，就使用预测控制量U*(hi+j|di),j=0,1,…,hi+1－hi－1。
　　（4）在di+1采样时刻，令di=di+1，重复步骤（3）。
3仿真验证
　　考虑高超声速飞行器的巡航条件(飞行速度V=13 Ma，飞行高度h=110 000英尺)，可以获取平衡点平衡点处初始状态和初始输入：x0=［459 0;0;33 528;0.023 3;0］T，u0=［0.164；－0.005 45］T。在该平衡点附近进行模型线性化处理，并以0.1 s的采样间隔进行离散化，获得离线时间线性模型系数矩阵：

　　采用常规预测控制［19］时，设定飞行速度和高度指令为30英尺/s和100英尺的阶跃指令信号，给定性能指标中的状态和输入的加权矩阵分别为Q=I5，R=0.1I2，预测时域N=10。将上述参数代入优化问题（式(10)）进行计算，得到如下的局部镇定控制率F和终端加权矩阵Ψ：

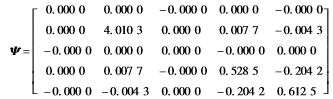
　　在双通道存在数据丢失，且最大连续丢包都为7(仿真步长为0.1)的情况下，最终得到高超声速飞行器系统输出响应如图3所示。

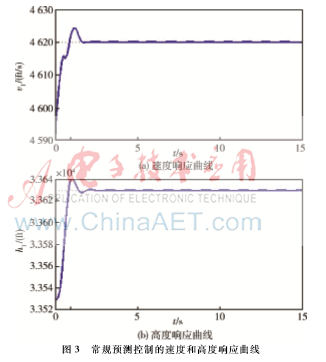
　　在上述参数不变的情况下，采用本文的补偿预测控制方法系统输出响应如图4所示。

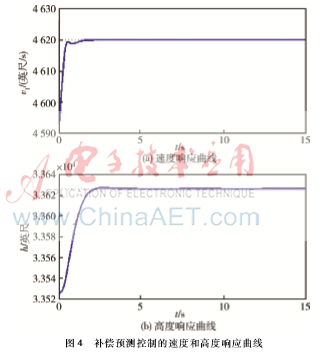
4结论
　　考虑存在数据丢失的高超声速飞行器巡航时的控制问题，运用了一种带有终端状态约束集和终端代价函数的预测控制器设计方法并设计相关的补偿策略。将控制器用于高超声速飞行器巡航段的控制中，仿真结果表明，飞行器在存在丢包时能够保持稳定飞行。
参考文献
　　［1］ 黄琳, 段志生, 杨剑影. 近空间高超声速飞行器对控制科学的挑战［J］.控制理论与应用, 2011, 28(10): 1496 1505.
　　［2］ Wang Qian, STENGEL R F. Robust nonlinear control of a hypersonic aircraft［J］.Journal of Guidance, Control and Dynamics, 2000, 23(4):577584.
　　［3］ SIGTHORSSON D O, JANKOVSKY P, SERRANI A, et al. Robust linear output feedback control of an airbreathing hypersonic vehicle［J］. Journal of Guidance, Control, and Dynamics, 2008, 31(4):10521066.
　　［4］ FIORENTINI L, SERRANI A, BOLENDER M A, et al. Nonlinear robust adaptive control of flexible airbreathing hypersonic vehicles［J］. Journal of Guidance, Control, and Dynamics, 2009, 32(2):402417.
　　［5］ 杨萌, 雷建和, 胡廷轩,等. 基于STM32的四旋翼飞行器控制系统设计［J］. 微型机与应用, 2015, 34(12):7679.
　　［6］ 高道祥, 孙增圻, 罗能, 等. 基于Backstepping的高超声速飞行器模糊自适应控制［J］. 控制理论与应用, 2008, 25(5): 805 – 810.
　　［7］ 王士星, 孙富春, 许斌. 高超声速飞行器的模糊预测控制［C］. 2013年中国智能自动化会议, 2013:2227.
　　［8］ 秦伟伟, 郑志强, 刘刚,等. 高超声速飞行器的LPV鲁棒变增益控制［J］. 系统工程与电子技术, 2011, 33(6):13271331.
　　［9］ Hua Chen, Li Ning, Li Shaoyuan. Switching multimodel predictive control for hypersonic vehicle［C］. Control Conference (ASCC), 2011 8th Asian, IEEE, 2011:677681.
　　［10］ 高海燕, 蔡远利, 唐伟强. 高超声速飞行器的调度离线预测控制［J］. 控制理论与应用, 2015, 32(2):224230.
　　［11］ 刘振华, 管萍, 刘小河. 高超声速飞行器的模型预测控制［J］. 北京信息科技大学学报(自然科学版), 2014(5):6266.
　　［12］ Hu Songlin, Yue Dong, Du Zhaoping, et al. Reliable H∞nonuniform sampling tracking control for continuoustime nonlinear systems with stochastic actuator faults［J］. IET Control Theory & Applications, 2012, 6(1):120129.
　　［13］ Dong Hongli, Wang Zidong, HO D W C, et al. Robust fuzzy outputfeedback control with multiple probabilistic delays and multiple missing measurements［J］. IEEE Transactions on Fuzzy Systems, 2010, 18(4):712725.
　　［14］ MARRISON C I, STENGE R F. Design of robust control systems for a hypersonic aircraft［J］. Journal of Guidance, Control, and Dynamics,1998, 21(1): 5863.
　　［15］ BRINKER J S, WISE K A. Stability and flying qualities robustness of a dynamic inversion aircraft control law［J］. Journal of Guidance Control & Dynamics, 1996, 19(6):12701277.
　　［16］ EPSTEIN M, Shi Ling, TIWARI A, et al. Probabilistic performance of state estimation across a lossy network［J］. Automatica, 2008, 44(12): 30463053.
　　［17］ Yu Junyan, Wang Long, Zhang Guofeng, et al. Output feedback stabilisation of networked control systems via switched system approach［J］. International Journal of Control, 2009, 82(9):16651677.
　　［18］ Xue Binqiang, Li Shaoyuan, Zhu Quanmin. Moving horizon state estimation for networked control systems with multiple packet dropouts［J］. IEEE Transactions on Automatic Control, 2012, 57(9):23602366.
　　［19］ 付亮, 马亚磊, 蔡远利. 高超声速飞行器单因素融合鲁棒预测控制［J］. 飞行力学, 2015, 33(3):2126.