陈霄鹏，彭亚雄，贺松

　　(贵州大学 大数据与信息工程学院， 贵州 贵阳 550025)

摘要：随着时间的变化，人的声音也会发生变化。这对说话人的识别带来了一定的影响。通过研究发现，说话人识别的性能与时间有着线性变化的规律。传统的说话人识别系统使用GMMUBM模型并不能很好地学习出线性变化规律。由于概率线性判别分析（PLDA）对于类内与类间有着很好的线性区分度，所以为了解决线性变化的问题，选择概率线性判别分析的方法学习说话人识别中时变的线性变化规律。从实验结果看出，PLDA对于说话人识别的识别鲁棒性具有很好的提升。

　关键词：说话人识别；时变鲁棒性；GMM-UBM；PLDA

0引言

　　说话人识别即声纹识别，为生物特征识别的一种。而声纹这一概念从诞生之初就一直伴随着其是否随时间变化的质疑。经过多年的研究发现，声纹识别确确实实随着时间发生变化。早在2003年，Bonastre教授已发表论文指出说话人识别的时变问题。在实际的说话人识别系统中，声纹预留与声纹验证之间的时间间隔也带来了系统性能的下降。

　　在已有的研究中，浙江大学CNNT实验室设计了一个声纹打卡系统，记录了实验室成员每天打卡情况，其中在开始的50天里识别率为69.02%，在稍近的几天里识别率提高到了74.19%。同时提出了平滑化梅尔倒谱系数（Smoothing Mel Cepstrum Coefficient, SMFCC ）这种更稳定的特征提高时变鲁棒性。

　　清华大学语音和语言技术中心王琳琳博士以Fratio作为中间准则计算频带区分度从而提高其鲁棒性。同时还提出了性能驱动的频率弯折方法的特征提取算法。

　　以上研究都基于特征层面，并未涉及到模型层面，本文研究着重于模型层面。

1说话人识别的线性变化规律

　　随着时间的变化，人的声音也会发生变化，从而影响说话人识别的识别率。其识别率会降低，而这种降低类似线性变化。所以，假设说话人识别中不同时间的特征之间的线性相关，通过特征之间的相关系数可以判别两个特征之间的线性相关性。根据实验结果发现，相关系数都在0.7~1之间，也就说明特征与特征之间有着极大的线性相关性。而且相关系数随着时间的变化也有着相对的线性变化。实验结果如图1。

　　为了更加准确地描述时间变化的规律，最大可能排除音素没有对齐的影响，故而选择动态时间规整（Dynamic Time Warping, DTW）对特征进行分析。将动态时间规整后的两段语音求cosine距离，根据cosine距离观察两段语音的相似程度。实验结果表明，cosine距离随着时间的变化也呈现出相应的线性变化。实验结果如图2。

　　由以上两个实验结果可以得出，随着时间的变化，说话人识别的鲁棒性呈线性变化规律。

2概率线性判别分析

　　说话人识别是模式识别的一种，分为训练和识别两个阶段。训练可以认为就是将语音按照不同的人进行分类，每一类代表了一个人，识别就是将测试的语音与已经分好类的模型进行比对。在说话人识别中加入时间的变化，就要同时考虑同一类的变化，即类内的变化，以及类与类之间的变化，也即类间的变化。

　　线性概率判别分析［13］(Linear Discriminant Analysis，LDA)是一种将类内和类间的方差作为多维高斯分布的一种技术，它寻求方向空间最大的辨别力，因此非常适合支持类的识别任务。

　　假设训练数据为不同的I个人，且每个人有J个语音，xij表示第i 个人的第j个语音，则LDA模型可表示为：

　　xij=μ+Fhi+Gwij+ij（1）

　　此模型分为两个部分：第一个部分μ+Fhi只与每个个体的特征有关，而与每条语音的特征无关；第二个部分Gwij+ij指每个个体语音的不同以及代表个体内部的噪声。其中μ为训练数据集的总体平均数；矩阵F的列包含了个人之间子空间的主要成分；hi代表这个子空间的位置；矩阵G包含了个体内部子空间的主要成分；wij代表这个子空间的位置；ij定义为高斯对角线协方差Σ（残差）。从条件概率方面来描述式（1）的模型：

　　Pr(xij|hi,wij,θ)=x［μ+Fhi+Gwij,Σ］(2)

　　Pr(hi)=h［0,I］ (3)

　　Pr(wij)=w［0,I］(4)

　　式a［b,C］中，a为变量，b为期望，C为方差的高斯分布。式（2）~式（4）都是同样的高斯分布。

2.1训练阶段

　　训练阶段的主要目标是得到一组数据点xij，并且得到相应的参数θ={μ,F,G,Σ}。如果知道隐藏变量hi和wij的值，这个问题将变得十分简单。同样地在给定θ的情况下也很容易估计hi和wij。但是式（1）中的很多参量都是未知的。

　　使用EM算法［45］可以解决这个问题。EM算法通过迭代轮流估计两个参数。在Estep，计算出整个后验分布中的隐藏变量hi和wij，从而修正参数的值。在Mstep，使参数θ={μ,F,G,Σ}的点估计最优化。

2.2识别阶段

　　在识别阶段，需要比较数据在R个模型M1…R下的似然分。定义模型M代表了隐藏身份变量hi和数据的一种关系。如果测试集中的多条语音属于同一个人，那么这些语音就需要一个相同的身份变量hi。反之如果多条语音对应了多个人，那么就需要不同的身份变量。因此需要得到第q个模型的似然分Pr(X|Mq)，其中X是所有的观察数据。为了计算每个模型的后验概率，需要使用贝叶斯准则［68］：

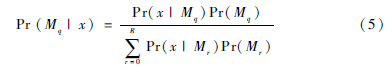
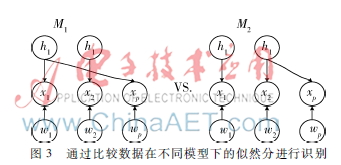
　　为了更真实地描述这个公式，假设训练语音为x1、x2,测试语音为xp。如图3所示，图中有两个模型，模型M1的测试语音xp与训练语音x1相匹配，则它们有着相同的身份变量h1［910］。同样地，模型M2的测试语音xp与训练语音x2相匹配，则它们就有着相同的身份变量h2。用下式计算数据在模型M1下的似然分：

　　Pr(x1,2,p|M1)=Pr(x1,p|M1)Pr(x2|M2) (6)

　　其中随机变量x1,p和x2是相互独立的。此处目标是求出观测数据的似然分，然而隐藏变量h和w都是未知的［1011］。提取出所有关键的观测似然分和已知的隐藏变量，忽略未知的隐藏变量，从而可以得到：

　　Pr(x1,p|M1)=Pr(x1,xp,h1,w1,wp)dh1dw1dwp(7)

　　进一步可以得到：

　　Pr(x1,p|M1)=∫［∫Pr(x1|h1,w1)Pr(w1)dw1

　　∫Pr(xp|h1,wp)Pr(wp)dwp］Pr(h1)dh1(8)

　　同样地，可以得出关于x2的条件概率：

　　Pr(x2|M1)=Pr(x2|h2,w2)Pr(w2)dw2Pr(h2)dh2(9)

　　以上条件概率所描述的都是最开始所定义的高斯分布，即式（1）~式（4）。同样地，模型M2可以用相同的方法做分解。

　　在计算式（8）、式（9）的积分时，算出N条语音匹配相同参数h的似然分，同时忽略了噪音参数w1...wN，加之PLDA是一种线性的高斯分布，所以可以将N条语音识别的系统按照式（1）写成下面的等式：

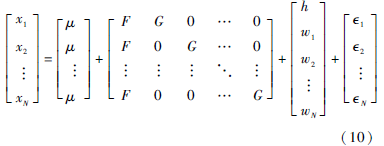
　　将上式重新命名为：

　　x′=μ′+Ay+′（11）

　　Pr(x′|y)=x′［Ay,∑′］（12）

　　Pr(y)=y［0,I］（13）

　　其中：

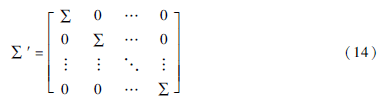
　　式（12）、式（13）即为标准的因素分析形式，而这种方法是已知的：

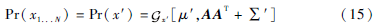
　　实际中，在已知矩阵A结构的前提下，可以提高计算效率。

3实验

　　实验采用GMM-UBM与PLDA进行比较。两种算法均采用采样率为16 kHz的语音和39维的MFCC特征，MFCC特征由基本的13维MFCC特征加上其一阶导数和二阶导数组成。其中MFCC的帧宽为24 ms，帧移为12 ms，预加重系数为0.97，MFCC滤波器组数目为30，低频截止频率为60 Hz，高频截止频率为3 600 Hz，DCT数目为16。同时增加有效语音检测(Voice Activity Detection, VAD)，取得有效音。对连续四周的语音进行测试，以等错误率（Equal Error Rate, EER）为判别标准。EER为错误拒绝率（False Rejection Rate，FRR）和错误接受率（False Acceptance Rate，FAR）相等的点。实验结果如表1。

　　其中本周测试表示以当前周的训练语音建立模型，用当前周的测试语音进行测试。第一周的结果表示的是以当前周的语音为训练语音，以当前周的下一周的测试语音进行测试。后三周的测试方法与第一周的测试方法相同。

　　由表1实验结果可以看出，说话人识别的时变鲁棒性具有线性变化规律，随着时间的推移，不论是GMMUBM［12］还是PLDA［13］，在不同周的测试效果均在逐步降低，但是PLDA的整体效果均优于GMMUBM。从时变的鲁棒性来看，PLDA的EER从第一周到第四周表现比较平稳，均保持在9%左右，而GMM_UBM在第三周开始有了明显的增加，也就是说GMMUBM的鲁棒性有所降低。

4结束语

　　本文通过使用PLDA模型对说话人识别进行了测试，目的在于解决时变的鲁棒性问题，从实验结果来看，PLDA对时变的鲁棒性有很大的提高。本文中使用PLDA和GMMUBM对语音进行了测试，以GMMUBM为基线，从测试结果来看，PLDA的整体效果均优于GMMUBM。以后可以使用PLDA为基线，通过对PLDA的改进来进一步提高时变的鲁棒性。

参考文献

　　［1］ YOUNG S. A review of largevocabulary continuousspeech recognition［J］. Signal Processing Magazine, IEEE, 1996, 13(5): 45.

　　［2］ LIANG L, RENALS S. Probabilistic linear discriminant analysis for acoustic modelling［J］. IEEE Signal Processing Letters, 2014,21(6):702706.

　　［3］ CHEN L F, LIAO H Y M, LIN J C, et al. A new LDA-based face recognition system which can solve the sample size problem［J］. Pattern Recognition, 2000, 33（10）: 17131726.

　　［4］ RUBIN R, THAYER D. EM algorithms for ML factor analysis［J］. Psychometrika, 1982,47(1):6976.

　　［5］ GHARAMANI Z, HINTON G E. The EM algorithm for mixtures of factor analyzers［R］. University of Toronto Technical Report, 1997.

　　［6］ DEHAK N, KENNY P J, DEHAK R, et al. Frontend factor analysis for speaker verification［J］. IEEE Transactions on Audio, Speech, and Language Processing, 2011, 9(4): 788798.

　　［7］ KIM T, KITTLER J. Locally linear discriminant analysis for multimodally distributed classes for face recognition with a single model image［J］. PAMI, 2005, 27(3): 318327.

　　［8］ MATEJKA P, GLEMBEK O, CASTALDO F, et al. Fullcovariance UBM and heavytailed PLDA in i-vector speaker verification［C］. In Proc. ICASSP. IEEE, 2011: 48284831.

　　［9］ HASAN T, HANSEN J H L. Acoustic factor analysis for robust speaker verification［J］. IEEE Transactions on Audio, Speech, and Language Processing, 2013, 21(4): 842853.

　　［10］ KENNY P. Bayesian speaker verification with heavy tailed priors［C］. In Speaker and Language Recognition Workshop (IEEE Odyssey), 2010：141.

　　［11］ GODFREY J J, HOLLIMAN E C, MCDANIEL J. SWITCHBOARD: telephone speech corpus for research and development［C］. In Proc. ICASSP. IEEE, 1992: 517520.

　　［12］ REYNOLDS D A, QUATERI T F, DUNN R B. Speaker verification using adapted Gaussian mixture models［J］. Digital Signal Processing, 2000, 10(1/3): 1941.