摘 要： 针对PID难以适应多种工况需求的问题，研发了一种新型控制器-智能轨迹导引控制器（Intelligent Track Guiding Controller）。ITGC汲取了经典PID的精髓以及自抗扰控制器（ADRC）思想，即在经典PID框架中引入“合理的过渡过程”，将提取到的微分信号的误差信号按照“适当的组合方式”来改善控制器功能和闭环系统的品质。ITGC具有结构简单、实现方便、参数易调整等优点，可以用来控制一般工业对象。温控实验结果表明，ITGC可以按照引导曲线控制温度达到设定值，整个过程无超调产生，并且能够应对各种扰动，具有良好的鲁棒性。

　关键词： ITGC；PID；温度控制；鲁棒性

0 引言

　　在实际的工业过程控制中，PID控制器仍占据着举足轻重的位置。究其原因主要是：（1）控制目标和对象实际行为之间的误差容易获取，而且能够适当加以处理，因而这种“基于误差来消除误差”的控制策略得到广泛的应用；（2）对于实际控制工程，通常很难给出其“内部机理描述”或者计算出的状态空间方程具有较强的针对性，所以基于数学模型的现代控制理论在实际工程应用中难以得到广泛应用[1]。尽管PID控制器大量应用于工业现场，但它并不能完全适应不同的工况要求[2]。因此很多专家学者对PID控制器进行了各种改进，如非线性PID控制器、自适应PID控制器、基于遗传算法的预测自整定PID控制器、模糊推理PID控制器[3]等。为了进一步改善PID控制器在不确定系统中的控制效果，韩京清教授提出了自抗扰控制器的概念[4]，明确提出了按照给定的目标轨迹来施加控制力的思想。本文汲取基于误差来消除误差的精髓结合ADRC引导控制的思想提出了智能轨迹导引控制器（Intelligent Track Guiding Controoler，ITGC）。

　　ITGC在继承PID不依赖受控对象数学模型和简化ADRC的基础上，采用一阶惯性环节的阶跃响应曲线取代原阶跃给定，将传统的“目标控制”改为“过程控制”，使被控对象实际值与阶段目标值之间的误差控制在合理的范围内，让被控对象平缓地到达最终设定值。这样不仅可以避免初期误差过大导致系统失控还可以减少超调量，满足快、准、稳的工艺要求。

　　本文首先介绍ITGC的结构原理，分析ITGC算法实现，然后使用MATLAB对ITGC与PID进行模拟仿真比较，最后将ITGC应用于温度控制实验，并加以扰动以验证其鲁棒性。

1 ITGC的结构原理

　　ITGC系统结构图如图1所示。

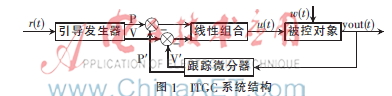
　　其中，P为位置给定信号，V为速度给定信号，P′为被控对象实际位置信号，V′为被控对象实际速度信号。

　　引导曲线由引导发生器产生，本文选取一阶惯性阶跃响应曲线作为引导曲线。

　　不同的被控系统有不同的时间系数T，参数的确定方法将在下一节介绍。

　　将引导曲线分解为两个给定信号：一个是“位置”给定信号，另一个是“速度”给定信号。将给定的位置信号与实际的位置信号做差作为“位置差”，给定的速度信号与实际的速度信号的差作为“速度差”，以位置差与速度差代替传统意义上的误差进行控制调节。即通过使用引导曲线，将误差取成：

　　e（t）=r′（t）-yout（t）（2）

　　其中r′（t）为某一时刻的引导值，这样保证了误差一直保持在合理的范围内，实现目标控制向过程响应之间的转换，让整个调节过程变得“平稳而柔和”，避免初始阶段较大的差值与较强的控制输出，保证了控制的平稳性。

　　2 ITGC算法实现

　　采用增量式方程输出：

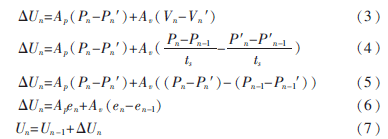
　　式（6）中，AP和Av分别为对位置控制的权重系数和对速度控制的权重系数，从算法本质上说ITGC是一个随动的PI控制器。本算法对原PI项进行换位调整：PID增量式中的比例项调节对应ITGC算法中的速度调节项；PID增量式的积分调节项对应ITGC算法中的位置调节项。虽然看上去相似，但实际上之所以ITGC控制器比PID控制器优越，在于它将传统PID算法的误差引申为“位置信号”与“速度信号”，规避了传统PID控制器在控制的初始阶段或者强干扰小的大误差下造成的控制输出紊乱、大幅震荡甚至系统崩溃。ITGC算法优势在于用小误差来引导控制输出，所以即使在大时间常数的控制系统中，对阶跃信号的响应也可以使过渡过程平缓而柔和，抑制了超调和振荡。

　　AP是位置项权重系数，只要给定引领曲线与被控对象的实测值之间存在误差en，则位置的控制作用就会发生作用。但是由于ITGC控制器的算法原理决定了位置误差不会很大，所以在整个系统调节过程中位置项的调节强度不会很大。

　　Av是速度项权重系数，只要给定引领曲线与被控对象的实测值之间误差的变化率在变化，则速度的控制作用就会发生作用。与PID控制器的微分相似，Av与误差的变化量有关，相当于加速度。但是速度控制不能消除静差，它必须与位置控制相互配合才能达到理想的控制效果。

　　在经典控制理论中，一阶惯性系统的阶跃响应曲线是一条初始值为零，以指数规律上升到设定值的曲线。它有一个非常重要的特点：可以用时间常数T去衡量系统输出量的数值。例如当t=T时系统的输出值将等于终值的63.2%；当t=2T时系统的输出值将等于终值的86.5%；当t=3T时系统的输出值将等于终值的95%。一阶惯性系统动态性能指标的调节时间为3T。

　　在实际的工业控制的参数整定中，在系统稳定的情况下施加一阶跃信号，让执行器以100%强度进行执行，当被控对象的测量值达到阶跃变化量的63.2%时，此时所用的时间就是被控对象的时间常数T，而整个ITGC控制器的调节时间为3T。

　　综上所述，ITGC只需确定3个参数：位置权重系数AP、速度权重系数Av、被控对象的时间常数T。

3 模拟仿真

　　从对象的开环响应曲线来看，大多数工业过程都能用一阶惯性加纯滞后（First Order Plus Delay Time，FOPDT）模型来近似描述[5]。基于这一点，可以假设工业对象模型的传递函数为：

　　3.1 阶跃实验

　　以稳定状态为1为例，设定值的阶跃响应如图2所示。

　　在模拟仿真实验中，实验时间为800 s，PID控制是典型的两波半，在300 s时系统稳定；ITGC在100 s时达到设定值，整个过程平滑无超调产生。

　　3.2 扰动实验

　　假设对象受n（t）方波扰动，在500 s时受到幅值为0.1的方波n（t）扰动信号，扰动时间为500~550 s。如图3所示。

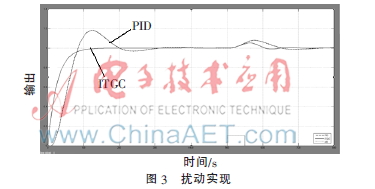
　　在模拟仿真实验中，实验时间为800 s，在方波扰动下，PID与ITGC都可以恢复到稳定状态，但ITGC的波动值明显低于PID，显示出良好的抗干扰能力。

　　通过仿真实验表明，经典PID可以实现稳定控制，也可以应对系统外来的干扰，但智能引导控制可以更快地实现对系统的稳定控制，超调更小，且具有良好的鲁棒性和抗干扰能力。

4 温控实验

　　4.1 硬件设备

　　温控实验设备由触摸屏、PLC、温控箱组成。温控箱中有温控模块、灯泡、风扇、PT100等。

　　触摸屏可显示温度变化曲线与调整控制参数；PLC用来温度采集与控制继电器和温控模块；温控箱可内置灯泡加热以及风扇加扰；温控模块可根据PLC中传出的值输出0~220 V电压；灯泡用来加热；风扇运行时施加扰动；PT100采集温控箱内的温度。

　　4.2 温控实验

　　设置目标温度为55 ℃，控制效果如图4所示。

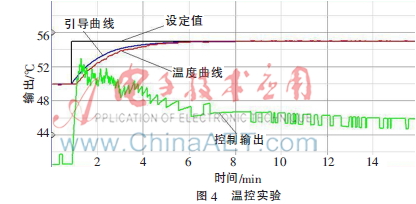
　　从图4可以看出，温度曲线可以紧跟引导曲线，从实验开始到温度稳定在55 ℃用时约6 min，无超调产生。最终设定值、引导曲线、温度曲线三线合一，控制效果稳定。

　　实际证明，ITGC不需要精确的数学模型，具有超调小、收敛速度快等特点。

　　4.3 加扰实验

　　在系统运行稳定的情况下分别进行阶跃实验与扰动实验。

　　4.3.1 阶跃实验

　　系统稳定在50 ℃，分别给系统施加上阶跃与下阶跃信号，以此验证ITGC对阶跃信号反应能力。控制效果如图5所示。

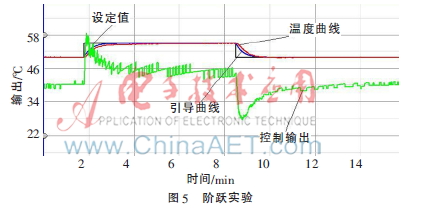
　　从图5可以看出，在加上阶跃信号的同时执行器立即产生变化，引导曲线开始上升，温度曲线可以紧跟引导曲线，最终设定值、引导曲线、温度曲线三线合一且无超调产生。在施加下阶跃信号的时候，系统也可以做出立即回应，最终设定值、引导曲线、温度曲线三线合一，控制效果稳定。

　　4.3.2 扰动实验

　　系统稳定在50℃，打开风扇施加扰动，然后关闭风扇，依靠系统自身来消除干扰，系统制效果如图6所示。

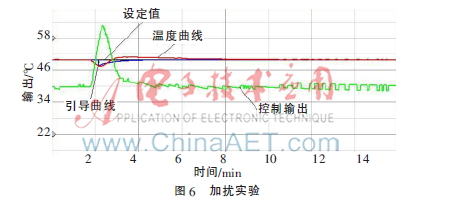
　　从图6可以看出，在风扇加扰的情况下，温度立即下降，而控制器也随之反应来阻止温度的变化，最终设定值、引导曲线、温度曲线三线合一且始终维持稳定。

　　从上述三个温度实验可以看出，ITGC完全可以满足温度控制系统的要求而且可以有效应对各种干扰，并将系统恢复到初始状态，具有很好的抗扰能力。

5 结论

　　本文利用经典PID的误差控制不依赖被控对象数学模型的优点，与ADRC的引导控制策略相结合，设计出一款依靠控制力来驾驭被控对象且不需要被控对象数学模型的简单控制器——ITGC。通过温控实验表明，ITGC对被控对象具有良好的控制力，可以引导被控对象平稳、快速地到达设定值且无超调；ITGC能有效地对抗扰动因素，具有良好的鲁棒性。对于ITGC的进一步完善，可以从参数寻优入手。ITGC已经在实际工业中得以成功应用，例如恒温水浴温度控制、炉膛负压控制、蒸汽压力控制等。可以将ITGC推广到冶金、交通、水利等行业，具有良好的行业推广性。

参考文献

　　[1] 韩京清.从PID技术到“自抗扰控制”技术[J].控制工程，2002，9（3）：13-18.

　　[2] 要晓梅，刘瑞英.一般工业对象的二阶自抗扰控制[J].控制工程，2002，9（5）：59-62.

　　[3] 罗运辉，刘红波，贾磊，等.一种基于DMC的新型预测PID控制器及其整定[J].控制理论与应用，2010，27（12）：1743-1749.

　　[4] P?魪REZ-CANO R， VRANCKX J J， LASSO J M， et al. Prospective trial of adipose-derived regenerative cell （ADRC）-enriched fat grafting for partial mastectomy defects： the RESTORE-2 trial[J]. European Journal of Surgical Oncology （EJSO）， 2012， 38（5）： 382-389.

　　[5] 赵彬，尤文.针对一阶惯性加纯滞后过程的模型算法控制研究[J].石油化工自动化，2008，44（1）：42-44.