摘  要： 随着数字技术的日益发展，应用在天文观测领域的数字信号处理技术也越来越成熟。本文针对ADC量化对于中性氢（HI）观测的影响进行研究分析。首先对HI观测进行了介绍性描述；在此基础上，对于使用实验室4.5 m天线进行HI观测时的信号接收处理系统进行了描述；重点对ADC量化以及射电望远镜灵敏度的相关公式进行推导，并结合4.5 m天线实际观测的数据处理结果进行对比说明，指出并证实了ADC量化位数不足带来的对于观测效果的影响可以通过提高积分时间得到补偿。

　　关键词： ADC；量化；中性氢谱线；灵敏度

0 引言

　　现阶段在很多地方都架设有用于天文观测的射电天文望远镜，架设地点通常会经过很多的选址对比，最终选择出一个相对适合的地点。而为了做测试而搭建的天线考虑到使用方便的因素，有些会选择在城市工作地点附近搭建。此时城市内的一些通信信号就成为了射电强干扰信号，给天文观测者带来了很大的影响。本文中4.5 m天线是架设在城市内的，针对中性氢谱线观测来进行讨论分析，目的是希望能够对将要在射电强干扰存在的情况下进行中性氢谱线观测的观测者提供一些参考，指出并证实ADC量化位数不足对于灵敏度的影响可以通过提高积分时间得到补偿。

1 中性氢（HI）观测的介绍

　　荷兰天文学家Vande Hulst在1944年提出了银河系中星系氢基态超精细结构跃迁谱线（对应氢的21 cm谱线）可以被观测到的预测。中性氢的观测开始于20世纪50年代Ewen和Purcell对于银河系中性氢谱线的观测，在此之后人们进行了大量的中性氢观测[1]。

　　用光学手段研究星际区域是很困难的，但是这些区域的氢原子却可以辐射21 cm谱线，并且不会被那些星际物质吸收，因此21 cm谱线成了探测宇宙空间的有力武器。通过观测可以详细地了解银河系中性氢的分布及运动规律，为精确地测量一些天体的距离奠定基础。高分辨率的中性氢观测也是研究星系相互作用的一个重要手段。

　　处于基态的中性氢原子，其电子自旋所产生的磁矩相对氢核自旋所产生的核磁矩有两种可能的取向：平行或反平行。前者的能量高于后者，当处于上能级的中性氢原子跃迁到下能级时，发出频率为1 420.406 MHz的光子，产生21 cm氢谱线辐射。在没有外界扰动情况下，它的自发跃迁概率很低，一个处于基态高能级的中性氢原子要在长达约1 100万年中才有一次跃迁到低能态的机会，导致了21 cm谱线的自然宽度很小[2]。

2 中性氢观测的信号接收过程以及观测设备介绍

　　观测使用实验室现有4.5 m口径的实验天线，信号经由单极性馈源喇叭接收后经过放大、滤波、混频等一系列模拟信号处理之后传输到实验室后端信号处理区域，将信号输入到由CASPER设计研制的接收机数字处理平台，此时信号中包含很强的通信用信号频段，对于中性氢观测来说这些通信宽频信号就是强度很大的射频干扰信号。接收到的模拟信号经过放大混频之后首先要输入ADC板卡来实现数字化，这是十分重要的一个步骤。经过ADC量化之后的信号实现了数字化，数字化的信号可以完全按照算法要求来进行后续的数字信号处理，从而得到HI谱线的观测结果。图1对应实验室4.5 m天线观测时信号接收处理过程。

　　基于CASPE硬件平台的谱线终端的实现是基于软件无线电的思路。中心思想是构造一个具有开放性、标准化、模块化的通用硬件平台，将各种功能（如多相滤波、频段获取、调制解调类型、数据格式、通信协议等）通过软件来实现。从基于硬件、面向用途的实现方法中解放出来。功能的软件化需要减少功能单一、灵活性差的硬件电路，特别是模拟环节，让数字化过程尽量靠近天线。采用开放性和可编程性的结构来改变硬件的配置结构[3]。

　　3 ADC量化对于观测灵敏度的影响分析[4-8]

　　ADC板卡是整个过程中十分重要的一环，它是连接着模拟和数字的环节。图2描述了ADC的结构图，前置的滤波器可以把输入信号中高于某一频率的频谱去除，以避免高频信号混叠到ADC的工作频带中。随后是抽样和保持电路，它可以对输入的模拟信号采样并在一个时间点保持不变，其目的是为了让后级的电路把这个固定的电平转化为所需要的数字编码，这个时间也叫做转换时间。转换的过程也就是量化的过程，在这个阶段把基准电平分成多个小的区间（例如N-bit的ADC就有2N个小区间）。在转换时间内找到与输入抽样电平相对应的量化区间，数字处理器就能够把它映射到对应的数字输出值，进行编码输出，得到最后的数字输出信号。

　　电路特性决定ADC的一些关键指标，例如采样和保持电路决定了ADC的精度和线性；量化器决定了ADC的分辨率；输出缓冲器决定了输出速率等。数模转换器的精度（分辨率）定义为模数转换器中用以描述一个模拟信号值所采用数字信号的位宽。N-bit的ADC用2N个不同的数值代表全量程范围的连续模拟信号值，通常用LSB（Least Significant Bit）表示。

　　下面推导N比特量化带来的影响。设VF为输入模拟信号的满量程电压值，P为量化电平，若ADC的位数为N bit，则有关系：

　　ADC实现的是用离散的数字量来表示连续的模拟量，所以这个过程中必然会引入一个因量化而带入的噪声。在用离散数字信号表示模拟量的过程中，因为在量化过程中存在着一个类似四舍五入的过程，因此，引入的量化噪声的最大量化误差可以达到P/2。若输入信号确定，并且假设输入信号在满量程的范围均匀分布，也就是在（-VF/2，VF/2）之间均匀分布，则量化噪声会在（-P/2，P/2）之间均匀分布，此处设定量化噪声信号为X，则有：

　　方差是随机信号在均值上下波动程度的一种统计特征，是用来说明随机信号各可能值相对于均值的偏离程度的一种运算，若定义X（t）为平稳随机信号，则有：

　　D[X（t）]=E[X2（t）]-E2[X（t）]（7）

　　设定信号X（t）为加在单位电阻上的噪声电流，则 E[X2（t）]表示消耗在单位电阻上的瞬时功率，包括交流和直流功率的一个平均值。E2[X（t）]可看作消耗在单位电阻上的等效直流功率。从而通过式（7）可知D[X（t）]表示消耗在单位电阻上的瞬时功率的交流部分平均值。

　　灵敏度对于射电望远镜来说是一个很重要的指标，通常是指望远镜能观测到的最小流量，用符号?驻T表示。在以下的推导计算中，Tsys是系统噪声温度，t是观测的积分时间，BW是观测的带宽，则有：

　　当观测射电源没有进入望远镜观测范围时，望远镜在观测带宽BW内的输入功率如下：

　　Poff=KTsysBW（9）

　　对应的功率的波动是：

　　当观测射电源进入观测范围时，由该射电源引起的接收功率的提升如果高于被观测源进入观测范围前的功率波动Poff，那么对于这个源的探测是一个可靠的探测。用Ptotal代表接收处理的总功率，Psource代表目标观测源带来的接收处理功率，而此时有：

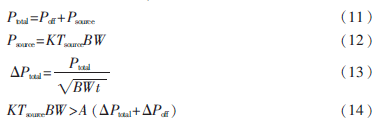
　　当式（14）中的A足够大（大于3）时，则认为被观测射电源是一个可以被可靠观测到的源。

　　对于经过ADC处理的电压信号，ADC器件的位数越多，则得到的电压值越精确。上面已经计算了量化误差引入的噪声影响，据此可以得到量化噪声引入功率Pn：

　　其中，N为ADC量化位数。可以看出f（N）=2×f（N+1），当量化位数足够多时，可以知道Pn十分小，从而Ptotal几乎不受影响。也就是说在这种情况下当ADC量化位数足够多的时候，量化带来的影响对于观测的影响很小，几乎可以忽略。但是在谱线观测的进行中，如果在观测频带内存在强的RFI（Radio Frequency Interference），情况将会发生很大的改变。在这种情况下，Tsys可以看成是随频率变化的函数。此时，因为ADC量化误差而引入的Pn带来的影响则发生了很大的变化，Ptotal因为强RFI的存在而发生了大幅度的提高，用P2表示有RFI的情况下的功率，用P1表示无RFI的情况下的功率，则有：

　　P1，total=P1，off+P1，source+P1，n（17）

　　P2，total=PRFI+P2，off+P2，source+P2，n（18）

　　当把整个谱线观测压缩到ADC的量化电压范围内时，各个量的变化如下：

　　P2，total>P1，total；P2，off<P1，off；P2，source<P1，source；P2，n=P1，n

　　对比有RFI存在的观测情况与没有RFI存在的情况，则有：

　　也就是说ADC量化噪声对于观测的影响变大了，在射电源信号十分微弱的情况下，这种变化可能会导致信号被淹没在噪声中。根据式（13）可知，提高积分时间可以提高系统的灵敏度而得到更好的观测效果，而ADC量化带来的影响是式（13）中Ptotal中的一部分，所以如果在有RFI的情况下进行观测，ADC量化带来的影响的加剧可以通过增加积分时间来进行优化。

4 观测分析证明

　　在中性氢信号比较强的时段使用4.5 m天线进行观测，ADC为8 bit，有效数据部分占用为4 bit，将数据进行32K个点的FFT，经过100 000次累加后得到如图3中虚线所示的谱线图，将数据进行1 bit量化得到新的数据进行同样的处理得到的谱线图如图3中实线图示，对比可以看出数据量化位数的降低，导致了信噪比明显的降低。图4是1 bit量化对应谱线数据与4 bit量化对应的谱线数据的比值，可以看出比值在对应中性氢信号频段发生了很明显的强于其余频段的下降，说明较低的量化位数的量化噪声带来的影响更为明显。

　　将4 bit量化的数据进行32K个点FFT，经过了1 000次叠加得到谱线如图5图示，100 000次叠加得到的谱线如图6图示，实际的数据处理结果证实了增加积分时间提高了信噪比，从而可以补偿低量化位数带来的对于观测的影响。

5 结论

　　在实验室进行调试时，窄带强干扰信号如果不经过合适的衰减，则会使ADC饱和，发生截断输出，从而使频谱输出波形发生严重的扭曲和变形。此时，必须增大对于输入观测信号的衰减，保证强干扰信号不饱和ADC，才能观测到正常的谱线。但是增加对于输入观测信号的衰减使强干扰信号不饱和ADC后，在HI观测频段，ADC器件本身器件的噪声就凸显出来，所要观测的HI信号被混在噪声之中。统计意义上说可以通过增加足够多的采样点来进行补偿，也可以理解为就是相应的提高积分时间来增加系统的灵敏度，这样仍然可以得到有效的观测结果。

参考文献

　　[1] EWEN H I， PURCELL E M. Observation of a line in the galactic radio spectrum： radiation from galactic hydrogen at 1，420 Mc./sec[J]. Nature， 1951，168：356.

　　[2] 钱磊.中性氢研究的前言问题[J].天文学进展，2011，29（4）：408-421.

　　[3] 杨小牛，楼才义，徐建良.软件无线电原理与应用[M].北京：电子工业出版社，2001.

　　[4] FELLI M， SPENCER R E. Very long baseline interferometry[M]. Netherlands： Kluwer Academic Publishers，1989.

　　[5] 周涛.量化精度对数字化接收机性能的影响[J].电子信息对抗技术，2006，21（6）：20-23.

　　[6] 李迪.高新能sigma-delta_ADC的设计与研究[D].西安：西安电子科技大学，2010.

　　[7] 史军，张乃通，王辉宇.UWB数字接收机量化阶数的研究[J].无线电工程，2008，38（2）：20-22.

　　[8] 姜碧沩.射电天文工具[M].北京：北京师范大学出版社，2008.