0 引言

网络传输能力由单位时间内成功传输的比特数表示，考虑到调制和编码对通信的制约，对文献[1]中的传输能力度量标准加以改进，目的在于利用受调制约束的传输能力指标来优化影响网络通信性能的主要参数。在调制指数和非相干检测技术的限制下，通过分析系统传输能力可知：跳频OFDM低压电力线通信网络中，网络通信中断概率是关于编码速率、调制指数和跳频信道数三个参数的函数。本文所分析的调制方式采用OFDM调制，同时采用高性能差错控制编码以受调制限制的传输能力作为目标函数，用于优化与上述三个参数有关的通信网络。对于跳频OFDM系统来说，可以考虑联合优化上述参数使得其性能相对最佳。因此，在分析跳频OFDM低压电力线通信网络性能的基础上，提出两种优化网络传输能力方法：穷举搜索法和梯度搜索法。穷举搜索优化法可优化大范围的离散参数，该方法优化精度高，但由于其完全优化性，使得在效率上存在缺陷，为此提出了一种梯度搜索优化方法以提高优化效率。

1 BPP模型中断概率

考虑某一固定能耗数据监测区域，该区域内存在一个呈环形分布的干扰信号区，干扰信号区域内半径为干扰最小距离，外半径为干扰最大距离，半径大小均由电力通信网络物理覆盖区域决定。通常监测区域节点数可以是固定的，也可以是随机的。在节点数固定的情况下，节点位置是实现二项式点过程（BPP）的关键；通信中断概率1_Ω是在已知归一化逆功率集Ω的条件下得出的，因此通信网络中各终端的地理位置对其有决定性影响，例如不同位置的干扰源。若要求得Ω未知情况下的非条件中断概率，可以对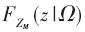在网络空间布局中求平均来实现。在BPP模型中，干扰源数目固定，且随机分布于网络任意位置该模型的中断概率1M可用条件中断概率对归一化逆功率集Ω的期望来表示：

本分析结果适合于接收终端和干扰源集中在环形区域内的网络，如要获得其他形状的网络中断概率，可以先求出合适的Ω_i累积分布函数，然后代入式(3)即可。

2 跳频OFDM电力线通信网络传输能力

在所允许的最大中断概率为ζ情况下，传输能力可表示为：

将式(6)代入式(3)可得BPP网络模型的传输能力：

假设一内外径分别为r_ex=0和r_net=2的BPP网络模型，路径损耗因子α=3，L′=1。信扰噪比阈值设为β=-10 dB。图1描述了3种信噪比情况下，传输能力参数关于最大允许中断概率的函数曲线，曲线由式(7)得到。由图可知传输能力随着信噪比的增加而提高。

上述分析得到的传输能力表达式是关于信扰噪比阈值β的函数。实际上，信扰噪比阈值可用关于调制方式和信道编码方式的函数来表示。设C(γ)是某一调制方式下瞬时信扰噪比为γ时所能达到的最大有效传输速率，则当网络传输速率R满足C(γ)≤R时，传输中断将发生。跳频系统采用OFDM调制技术时，不同调制指数情况下所能获得的最大有效传输速率如文献[2-4]所述。设OFDM调制指数为h，用C(h，γ)表示调制指数为h时的最大有效传输速率，令C(h，γ)=R求得的信扰噪比γ即为此时的信扰噪比阈值β。然而，实践证明实际传输中要求的β要比理论计算值稍高^[5-6]，高出的经验值约为1 dB。设η为调制的频谱利用率，单位为符号每秒每赫兹(S/s·Hz)，OFDM的调制效率可由归一化功率谱密度的数值积分获得。为了体现调制指数h对η的制约，后文用η(h)代表调制频谱利用率。若再考虑速率为R的信道编码，则频谱效率可由每秒每赫兹所传输的信息比特数Rη(h)表示，网络平均传输速率或吞度量T可表示为：

与式(3)不同的是，式(9)表述的网络传输能力考虑了编码率R、调制频谱效率η(h)和跳频带宽B/L′的影响。

3 跳频OFDM低压电力线通信网络优化

图2描述了归一化参数(R，L′，h)对传输能力的影响。信噪比固定为SNR=10 dB，(R，L′，h)的其中一参数变化，另外两参数恒定，图中每条曲线均对应一个参数值使得此时的传输能力最优。

4 梯度搜索网络优化

由图2可知：对于跳频OFDM电力线通信网络而言，网络性能好坏受跳频信道数、调制指数和编码速率的影响，为使跳频OFDM电力线通信网络性能最优，需对跳频信道数、调制指数和编码速率进行联合优化。利用穷举搜索法时，最大归一化传输能力关于信噪比?祝的函数曲线如图3所示。

由于传输能力是参数(R，L′，h)的凹函数，穷举搜索优化实际是一种凸面优化。凸面优化可通过梯度搜索^[7]来完成。基于梯度搜索的通信网络参数优化方法步骤如下：

(3)在集合β_set中任取一个β；

　　(4)在集合h_set中任取一个h，利用R=C(h，?茁)求出当前β下的传输速率和频带利用率η(h)；

　　(5)对集合L_set中所有的L′值，利用式(16)计算步骤(3)和(4)确定的h和R所对应的τ^′(λ)；

(6)判断最大τ^′(λ)所对应的L′值：

①如果最大τ′(λ)所对应的L′值是极值之一，就将中间值向该极值方向移动并更新极值使其距新中间值更近；

②如果最大τ′(λ)所对应的L′值是中间值，直接更新极值使其距原中间值更近。

(7)用新集合重新执行步骤(5)，直至极值间距足够小且中间值使得τ′(λ)最大；

(8)对集合h_set中所有的h值重复步骤(5)、(6)和(7)，并保存之前的最优TC和L；

(9)判断最大τ′(λ)所对应的h值：

①如果最大τ′(λ)所对应的h值是极值之一，就将中间值向该极值方向移动并更新极值使其距新中间值更近；

②如果最大τ′(λ)所对应的h值是中间值，直接更新极值使其距原中间值更近。

(10)用新集合重新执行步骤(8)直至极值间距足够小且中间值使得τ′(λ)最大；

(11)对集合β_set中所有的β值重复步骤(8)、(9)和(10)，并保存之前的最优TC和h；

(12)判断最大τ′(λ)所对应的β值：

①如果最大τ′(λ)所对应的β值是极值之一，就将中间值向该极值方向移动并更新极值使其距新中间值更近；

②如果最大τ′(λ)所对应的β值是中间值，直接更新极值使其距原中间值更近。

(13)用新集合重新执行步骤(11)直至极值间距足够小且中间值使得τ′(λ)最大，并保存此时的最优τ′(λ)和β值。

表1比较了同一BPP网络模型分别采用穷举搜索和梯度搜索的优化结果，针对不同的空间布局，分别考虑了r_ex=(0.25，0.5)、r_net=(2，4)和α=(3，3.5，4)多种情况。由参数可见梯度算法的优化效果与穷举算法相当。参数I_Δ为梯度搜索从初始化到结束所执行的循环次数，分析可知，不同情况下梯度搜索的循环次数变化不大，但穷举搜索其搜索循环次数会随参数变化而增加。因此，梯度搜索优化不但优化效果与穷举搜索接近，而且搜索优化效率明显增加。

5 结论

本文分析了跳频OFDM低压电力线通信网络的传输能力，求得了其通信传输中断率的闭式解，在分析传输能力理论表达式基础之上，以传输能力作为系统性能指标，提出穷举搜索和梯度搜索联合优化跳频信道数、OFDM调制指数和差错控制编码速率。分别给出了穷举搜索优化和梯度搜索优化的使用范围，实验证明穷举搜索和梯度搜索优化效果接近，梯度搜索的优化效率更高。

参考文献

[1] WEBER S，YANG X，ANDREWS J，et al.Transmission capacity of wireless ad hoc networks with outage constraints[J].IEEE Trans.Inform.Theory，2005，51(12)：4091-4102.

[2] TORRIERI D.Principles of spread-spectrum communication systems[M].New York，NY：Springer，second ed，2011.

[3] MOLLENAUER F.Mobile broadband wireless access proposal[P].IEEE 802.20 Working Group，IEEE P802.20-07/09r1，Mar，2007.

[4] CHENG S，SESHADRI R I，VALENTI M，et al.The capacity of noncoherent continuous-phase frequency shift keying[C].In Proc.Conf.on Information Sciences and Systems(CISS)，(Baltimore，MD)，March，2007.

[5] TORRIERI D，CHENG S，VALENTI M.Robust frequency hopping for interference and fading channels[J].IEEE Trans.Commun.，2008，56(8)：1343-1351.

[6] MASSE M R，MICHAEL B.Adaptive coding for frequency-hop transmission over fading channels with partial-band interference[J].IEEE Transactions on Communications，2011，59(3)：854-862.

[7] BOYD S，VANDENBERGHE L.Convex optimization[M].New York，NY：Cambridge University Press，first ed，2004.