LTE所选择的上行传输方案是一个新变量：SC-FDMA(单载波-频分多址)相比于传统OFDMA其优点是既有单载波的低峰均功率比(PAPR)，又有多载波的可靠性。在上行链路这点特别重要，较低的PAPR可在传输功效方面极大提高移动终端的性能，因此可延长电池使用寿命。代表LTE物理上行共享信道(PUSCH)的基带信号产生过程如图1所示[1]。

图1中的转换预编码是由一种对称形式DFT完成，其种类及变换长度L=2k1×3k2×5k3(L≤1 200)见表1。

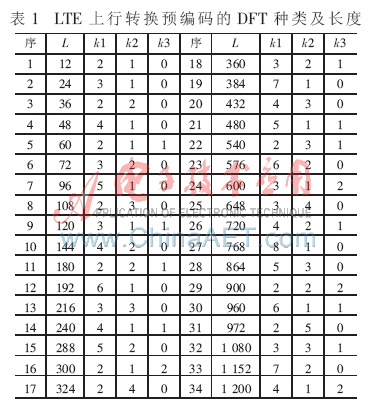
转换预编码是根据不同的输入长度L动态地执行表1中的一种DFT。其主要特点是包含的DFT种类多、规模庞大，这给硬件设计带来挑战。以前的文献大都以基2或单个混合基FFT[6]为重点进行阐述，而以多种混合基FFT为核心的文章还很难发现。本文提出一种基于FPGA的转换预编码解决方案。
1 算法选择
Cooley-Tukey算法和Good-Thomas算法是当前流行的FFT算法，文献[2]中已对其原理进行过深入讨论，这里不再赘述。
(1)Cooley-Tukey算法具有良好的模块性，并且可以实现原位计算，对输入数据以及旋转因子的抽取具有规律性。文献[3]提出的一种基3 FFT算法是Cooley-Tukey算法应用在基3 FFT中的另一种表述。这一算法区别于其他FFT算法的一个重要事实就是因子可以任意选取，通用性强，且所有的运算单元均相同，易于实现。
(2)Good-Thomas算法只适合因子互质的情况，由于避免了中间级乘旋转因子的运算，因此比Cooley-Tukey算法的运算次数少得多。FFT点数越大，越能体现其在节省资源方面的优点。
文献[4]提出一种基于Cooley-Tukey算法的传输预编码解决方案。此方案的优点是操作简单、模块规则、利于编程实现；缺点是需要做的级间旋转因子乘法较多(最多达几百)，乘法器和存储器等硬件资源开销较大，同时将大大增加系数初始化的工作量。对几种不同长度FFT运算量进行比较见表2。

表2中的混合算法指Good-Thomas算法与Cooley-Tukey算法相结合。可以看出，Good-Thomas算法与Cooley-Tukey算法相结合与文献[4]相比，减少了级间旋转因子乘法数，可以有效降低运算量，这些运算量的降低对整个系统的实现起着至关重要的作用，而其付出的代价只是复杂度的略微提升。
综上所述，在实现混合FFT时，选择Good-Thomas算法与Cooley-Tukey算法相结合，且优先选择Good-Thomas算法，其次为Cooley-Tukey算法，系统设计将从Good-Thomas算法出发。
2 总体结构设计
从表1中看出，LTE上行转换预编码要进行的FFT变换种类多，但每一种变换的架构是相似的，都是由基2及非基2点FFT的公共模块组成。基2有点数为4，8，16，32，64，128，256的模块，非基2的有点数为3，9，15，27，45，75，81，135，225和243的模块，只要抽出这些公共模块并精心设计，再合理地调用，就会顺利完成这个看似繁琐的工作。
图2所示总体结构框图中，模块A和C分别为数据输入和输出模块；模块B为数据处理模块，其主要思想是动态配置和公共模块的复用，内部FFT模块事先单独生成，MUX1，MUX2是选择器，在不同输入点数的情况下动态配置不同的内部FFT模块来组合成外层FFT，这样内部FFT模块就可以达到复用的目的，可以大大减少总体资源耗用，而处理速度也与单独执行各FFT相当。

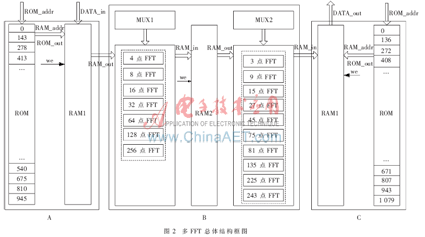
3 硬件实现
在实际应用中，一般由FPGA完成需要快速和较为固定的运算，由DSP完成灵活多变和运算量较大的任务[7]。XilinxVirtex-5SXT平台针对具有低功耗串行连接功能的DSP和存储器密集型应用进行了优化，具有硬件结构可重构的特点，适合算法结构固定、运算量大的前端数字信号处理，可以大量卸载这些功能，释放DSP带宽以处理其他功能，所有这一切都使得FPGA在数字信号处理领域显示出自己特有的优势。
3.1 地址映射
以1 080点FFT在图2所示系统中的实现过程分析系统工作原理。因为1 080=8×135，且8和135互质，故外层采用Good-Thomas算法。
输入地址映射：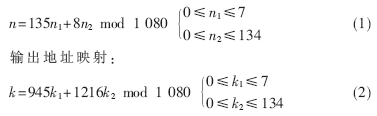

FPGA内嵌Block RAM的使用可以大大节省FPGA的可配置逻辑功能块（CLB）资源。Good-Thomas算法需要对输入输出数据进行排序，输入输出端处理方法相同，这里只介绍输入端处理。在输入端，鉴于Block RAM的特征，设置一个ROM和RAM，如图2模块A所示。对于不同长度的FFT，ROM不同，但RAM可以共用。在ROM里预先存放输入数据在RAM1中的位置序号，此位置序号由（1）式得到，在时钟沿到来时，先顺序读出存储在ROM中的位置序号，将此数作为RAM1的地址输入，就能将输入数据存放到RAM1中的不同位置。这样在输入数据的同时完成了数据的排序，一举两得。1 080点FFT的输入和输出端地址索引如图2所示，其逻辑时序图见图3。图3中，RAM_in由测试数据xn_i和xn_r进行位拼接后输入。

3.2 内部FFT处理单元
当进行图2模块B中的操作时，内部FFT模块先单独生成。Xilinx提供的FFT IP核适用于基2点的FFT变换，其所采用的算法为Cooley-Tukey算法，变换长度为N=pow2(m)，m=3~16，数据采样精度和旋转因子精度都为8~24，故模块B的8、16、32、64、128及256点FFT都可用IP核生成。选择“Pipelined,streaming I/O”生成基2点FFT模块，可以减少整体处理时间。15、45、75、135、225点FFT模块的外层算法是Good-Thomas算法，其余采用Cooley-Tukey算法实现。
具体到1 080点FFT，将RAM1中的数据顺序读出，由MUX1选择进行8点FFT变换，完成第一级操作后，所得中间结果顺序存储在RAM2中；然后再将RAM2中的中间结果取出，由MUX2选择进行135点FFT变换，共操作8次，完成第二级操作，所得结果按模块C中ROM指示的顺序存储在RAM1中；最后顺序输出RAM1中的内容就是1 080点FFT的结果。
3.3 乘法器设计
量化效应在数字信号处理技术实现时是很重要的问题，主要包括运算量化效应、系数量化效应等，前者的影响大于后者[5]。运算中还可能出现溢出，造成更大的误差。上述问题对乘法器的设计提出了要求，由上文知，基2 FFT由IP核生成，故此处的乘法器设计只针对非基2 FFT有效。
Xilinx的XC5VSX95T内部共有640个DSP48E，每个DSP48E包含一个25×18 乘法器。在调用乘法器IP时，将乘数设为宽度为25和18的signed型（旋转因子位宽为18），输出截取结果的[41：17]共25 bit，乘法器输入输出宽度相等，在结果输出的同时对结果进行缩放，这样利于程序模块化，但前提是要保证数据不溢出。由于输入采样数据宽度只有16 bit，而转换预编码输入数据最大长度只有1 200点，再考虑旋转因子系数小于1，可以断定25 bit位宽可使乘法器结果不溢出，且运算精度也可满足要求。
4 性能分析
程序利用Verilog HDL硬件描述语言编写，在Xilinx公司的高性能设计开发工具ISE10.1i中编译成功。当FPGA芯片选为XC5VSX95T时，在Synplify Pro 9.6.1中进行逻辑优化与综合后显示其最大时钟频率为105.6 MHz，FFs耗用29 150/58 880，LUTs耗用37 625/58 880，乘法器耗用414/640，Block Ram耗用176/488，各项指标都合符要求。布局布线成功后，在Matlab中产生一实正弦测试信号，经采样量化成1 200点数据后输入Modelsim SE 6.1d对程序进行后仿真，然后输出结果回送至Matlab，得到仿真图如图4。

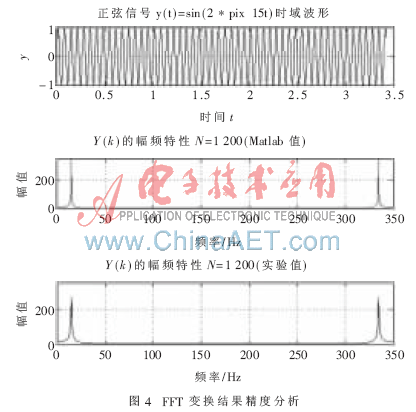
由图4可以看出FFT处理器处理后的结果和Matlab计算的理论结果基本一致，都在频率为15 Hz和335 Hz处取得最大FFT绝对值，两者之间的误差正是数字信号处理量化效应的体现。从整体看，这些误差是数据在经过采样量化和截断处理后不可避免的且是可以容忍的，因此可以判断测试结果符合精度指标。
本文讨论了应用在LTE上行转换预编码中的多种FFT的软硬件实现。与各种FFT单独处理或只采用Cooley-Tukey算法的方法相比，本设计巧妙地将Good-Thomas算法与Cooley-Tukey算法结合起来，在硬件资源和成本消耗上都有很大的节省，速度上也能满足要求，而且这种结构很容易进行功能扩展，只需要调整内部FFT单元的种类和数目即可。这种大规模混合基FFT的实现方法对其他场合的大规模FFT有一定的普适性。
参考文献
[1] 3GPP TS 36.211 v8.7.0：Physical Channels and Modulation(Release 8)[S].2009，6.
[2] Uwe Meyer-Baese.数字信号处理的FPGA实现[M].刘凌，胡永生译.北京：清华大学出版社，2003.
[3] SUZUKI Y，SONE T，KIDO K.A new FFT algorithm of radix 3, 6 and 12[J].IEEE Trans on Acoustics，Speech and Signal Processing，1986，4.
[4] MUNDARATH J.Mixed radix DFTs for LTE Uplink. Freescale Semiconductor，Inc，2008，6.
[5] CHANG Wei Hsin，TRUONG Q.On the Fixed-Point accuracy analysis of FFT algorithms[J].IEEE Trans on Signal Processing，2008，56(10).
[6] 吴松炎，管云峰，余松煜，等.非基2点FFT处理器的设计及实现[J].电视技术，2007.
[7] 李小文，李贵勇，陈贤亮，等.第三代移动通信系统、信令及实现[M].北京：人民邮电出版社，2003.