文献标识码:A
文章编号: 0258-7998(2014)01-0044-03
小波变换在时域、频域均有良好的分辨率[1],其应用广泛[2-3]。Morlet小波、Marr小波及DOG小波同属于高斯类小波,且从最大成度上解决了时宽和带宽不相容的矛盾,因而很多工程领域将高斯类小波函数作为母小波函数进行小波分析。开关电流电路是电流模信号处理技术,它用离散时间的取样数据系统处理连续时间的模拟信号。相比开关电容技术,开关电流技术不需要线性浮置电容,CMOS工艺兼容,具有大动态范围、良好的高频性能、高速度、低功耗等优良特性,有利于大规模电路集成[4-6]。本文提出了一个以频域中的高斯函数单元为核心的共享结构系统实现3种高斯类小波变换。在此频域共享结构实现方案中,复用频域高斯函数单元采用开关电流电路实现频域高斯类小波变换系统,不同尺度上的高斯类小波变换可通过调节开关电流电路的时钟频率获得,所提出的频域共享结构高斯类小波变换系统适合于制成通用型小波变换芯片。
1 小波变换频域法实现原理
小波变换频域表达式如下: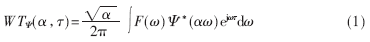
式中,ω为尺度因子,F(?棕)、?追(?棕)分别为信号与母小波函数的频域表达,?鄢表示共轭。频域小波变换表达的物理意义为:当尺度?琢连续变化时,信号的小波变换可等效为信号通过无限多个不同中心频率和带宽的带通滤波器。根据信号处理理论,信号与某个函数的卷积就是信号通过以该函数特性为冲激响应系统的输出。这样,只要构造冲激响应为不同尺度小波函数的滤波器组,则信号通过该滤波器组后的输出就是信号的小波变换。由此,小波变换的实现转化为构造冲激响应为不同尺度小波函数的滤波器组[7],这样可将小波变换从时域变换到频域实现。值得关注的是,在构造不同尺度与位移的小波函数滤波器时,要保证中心频率与频宽(带宽)之比(也即品质因数Q)与尺度ω值无关。小波变换具有冗余性,尺度ω不需连续变化,实际应用只需将尺度ω离散化即可,如取ω=2n(n∈Z)。图1为小波变换的频域法系统实现。



图5所示电流域RLC跳耦高斯滤波器的阻抗函数与导纳函数可用开关电流双线性积分器综合实现[6,9],进而得到开关电流高斯滤波器。
4 频域高斯类小波变换共享系统仿真
根据提出的频域共享结构高斯类小波变换系统,采用开关电流技术电路实现高斯滤波器及其他所需系统模块,并进行系统级仿真,仿真工具为Matlab。系统级仿真在a=20尺度、a=21尺度、a=22尺度上进行,图6为高斯函数单元的频率响应仿真结果。通过移频单元后实现Morlet小波变换,图7为其频率响应仿真结果。Marr小波和DOG小波的频率响应仿真结果分别如图8、图9所示。图2所示频域共享结构仅给出a=20尺度、a=21尺度及a=22尺度的高斯类小波变换实现,通过增加频域共享结构组合模块的数量,可完成更多尺度上的频域高斯类小波变换。


因为同时在时域、频域具备良好的分辨率,工程领域常常应用同属高斯类小波的Morlet小波、Marr小波、DOG小波作为母小波完成小波变换。本文提出了一个以频域中的高斯函数单元为核心的频域共享结构系统实现高斯类小波变换,以开关电流技术完成频域共享系统的电路实现,通过调节开关电流电路的时钟频率,可完成不同尺度上的高斯类小波变换。共享结构的提出可在最大程度上减小电路规模,为降低芯片功耗提供了有利条件,便于制成通用型高速低功耗小波变换芯片。所提出方法具有相当大的理论价值与实际意义,其有效性得到了仿真结果的验证。
参考文献
[1] STEPHANE M.A wavelet tour of signal processing (Third edition:the sparse way)[M].New York:Academic Press,2008.
[2] 范玉庆,王小华,曹志锋,等.小波变换与概率神经网络的心电图分类[J].电子技术应用,2013,39(3):136-137.
[3] 李立言,赵民建,钟杰.一种基于小波降噪的GNSS轨迹平滑算法[J].电子技术应用,2012,38(10):118-121.
[4] TOUMAZOU C,HUGHES J B,BATTERSBY N C.开关电流—数字工艺的模拟技术[M].姚玉洁,刘激扬,刘素馨,等译.北京:高等教育出版社,1997.
[5] 王友仁,祝呜涛,任晋华,等.面向多功能模拟信号处理的开关电流型可重构模拟电路研究[J].电子学报,2011,39(5):1047-1052.
[6] 李目,何怡刚.基于开关电流双线性积分器的IFLF小波滤波器设计[J].电路与系统学报,2013,18(2):191-195.
[7] 胡沁春,何怡刚,郭迪新,等.基于开关电流技术的小波变换的滤波器电路实现[J].物理学报,2006,55(2):641-647.
[8] 胡沁春,何怡刚,李宏民,等.基于开关电流的连续小波变换实现[J].湖南大学学报(自然科学版),2005,32(5):
66-70.
[9] 胡沁春,何怡刚,郭迪新.基于开关电流的Morlet小波变换及重构的实现[J].电子测量与仪器学报,2006,20(2):5-9.

