摘 要：根据离散小波变换原理的特点，提出了一种基于DWT域的数字水印算法，并用FPGA硬件实现其中关键部分的DWT变换。详细介绍了相关模块的设计和时序，并对整个系统进行了综合仿真，验证了设计的正确性。分析与仿真结果表明，与软件实现相比，用FPGA实现水印算法具有高速实时处理的优点。
关键词：DWT； 数字水印； FPGA

随着计算机网络和通信技术的飞速发展，数字媒体（包括数字图像、数字视频、数字音频）已得到了广泛的应用，随之而来的数字媒体的信息安全、知识产权保护和认证等问题也变得日益突出。数字水印作为传统加密方法的有效补充手段，是一种可以在开放的网络环境下保护版权和认证来源以及完整性的新技术[1]。
根据水印的实现过程，图像水印算法可分为空域算法和变换域算法。空域算法是通过直接改变原始图像的像素值来嵌入水印，通常具有较快的速度，但鲁棒性差，且水印容量也会受到限制；变换域算法是通过改变某些变换系数来嵌入水印，通常具有很好的鲁棒性和不可见性,其实现一般基于图像变换(如DCT、DFT、DWT等)。大多数水印算法采用软件实现,软件实现具有易于应用、升级和适应性较好等特点，但存在速度受限、难以满足实时处理的问题。而采用硬件实现则可以克服这些问题。本文基于上述考虑，利用FPGA设计了基于DWT(Discrete Wavelet Transform)域的数字水印算法，其中提升小波变换是该数字水印方案的关键单元之一，采用硬件描述语言Verilog HDL对算法进行描述，并用ModelSim完成了功能和时序仿真。
1 离散小波变换原理
1.1 Mallat算法及提升格式
1987 年,Mallat将计算机视觉领域的多分辨思想引入了小波分析，提出了多分辨分析MRA(Multi-resolution Analysis)的理论，并给出了数学描述和一种子带滤波器的离散小波变换与重构算法——Mallat算法。在图像处理领域,需要处理的通常是二维图形。因此,将Mallat算法扩展到二维空间, 适当地选取一组行和列变换正交的小波系数,对图像(或分解后的低频子图)分别进行行变换和列变换。然后,根据后续的具体应用对N次分解所得的图像在不同的分辨率下进行分析、处理或数据压缩。二维Mallat算法的结构如图1所示。

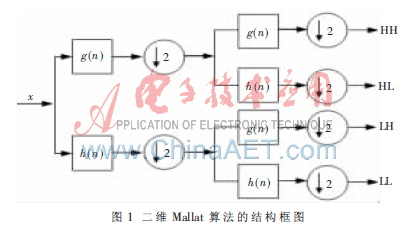
首先,用滤波器组g(n)和h(n)对图像的每一行信号进行滤波和2抽取,然后用相同的滤波器组对所得结果的每一列再次进行滤波和2抽取。这样,原始图像就被分解成为4个子带图像,分别表示为LL、LH、HL和HH。其中,LL为水平和垂直方向的低通信号;LH为水平方向低通,垂直方向高通;HL为水平方向高通,垂直方向低通;HH为水平和垂直方向的高通信号。
相对于Mallat算法而言，提升算法[2]是一种更快更有效的小波变换方法，标准的提升算法包含分裂(Split)、预测(Prediction)、更新(Update)三个步骤。分裂是将输入数据分为偶数序列和奇数序列两个部分;预测是用分裂的偶数序列预测奇数序列,得到的预测误差为变换的高频分量;更新是由预测误差来更新偶数序列,得到变换的低频分量。提升算法的结构框图如图2所示，其提升实现过程由式(1)和式(2)表示，其中滤波系数α=-1/2, β=1/4。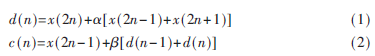

本文将采用5/3小波滤波器来实现小波变换。
1.2 边界处理
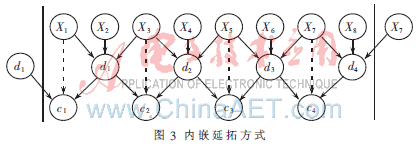
由于图像数据是有限长的，因此离散小波变换必须对图像数据进行边界延拓，在做小波提升算法时，同样需要对其边界数据进行延拓，以保证边缘数据的正确。基于资源消耗和功耗的考虑，这里采用内嵌对称延拓提升算法[3-4]，将延拓的过程融合到提升变换过程中。精简后的内嵌延拓方式如图3所示，其中Xn表示图像数据，dn表示高频分量，cn表示低频分量。

2 数字水印方案的设计
基于小波的图像水印算法有很多，本文采用LSB方法[5]直接将水印信号嵌入到经过小波变换的子图中，这里所用到的水印信号是由线性移位寄存器产生的m序列。图像经过小波变换后，低频子带 LL 表示为 L(n)，数字水印序列设为a(n)，在低频子带中嵌入水印序列，算法如下：

其中α为常数，当水印序列为“1”时，对子带数据加α；当水印序列为“0”时，对子带数据减α。
整个设计过程的核心为提升小波变换的FPGA的实现。根据二维小波变换的特点，将总体设计分为水平一维DWT 单元、垂直一维DWT单元、外部存储单元和控制单元。总体设计框图如图4所示。

2.1 二维DWT单元
二维提升式小波变换可以分解为两个一维小波变换，先进行行方向的离散小波变换，再进行列方向离散小波变换，这样就可以完成二维提升式小波变换。在本设计中采用的是并行的二维提升离散小波变换，根据提升式小波变换的特点，当列变换处理完三行数据后，即可以进行行方向的变换。因此可以根据二维小波变换[6]这个特点，使用四行缓存来缓存列方向小波变换后的系数。在第三行缓存存满后就开始从左向右进行“行方向”小波变换。因为在进行行方向小波变换的同时，仍然在进行列方向的小波变换，所以需要第四行缓存继续缓存列方向变换得到的小波系数以避免数据的丢失。通过以上的处理，实现了并行的二维离散小波变换，极大地提高了小波变换的速度。在这整个架构包含了列方向小波变换模块及其控制模块、行方向小波变换模块及其控制模块，以及用于缓存一维小波系数的缓存组。其中列方向变换模块在列方向变换控制模块的控制下，从系统外部读入影像数据进行列方向小波变换处理，并根据列变换的控制信号将处理后得到的小波高、低频系数存储到系统内部缓存中。行方向变换模块在行方向变换控制模块的控制下，从缓存器中取出列方向小波变换处理后的小波系数，进行行方向小波变换处理，得到二维小波变换后的LL、LH、HL、HH小波系数，最后输出到系统外。
2.2 存储单元
在变换过程中，首先对图像数据进行行方向的一维提升式小波变换，将变换后的数据存放在存储器或临时寄存器中，行方向变换结束后，再对该存储器中的数据进行列方向变换。这里使用的是FIFO存储器。FIFO是一种先进先出的存储器，就好像一个单向管道，数据只能按照固定的方向从管道一头进来，再按照相同的方向从管道另一头出去，最先进来的数据必定最先出去。
2.3 控制单元
控制单元接收外部控制信号(芯片使能、数据时钟等),由内部计数器进行计时、产生水平一维DWT 单元、垂直一维 DWT 单元和存储单元的控制信号(模块使能、起始终止信号等),对外部数据或前一级的LL输出数据进行锁存、处理、缓冲、输出等操作。
3 实验结果
在整个电路设计过程中,采用Verilog HDL语言对二维小波变换结构进行了RTL设计，并且采用ModelSim仿真对设计进行验证，其结果与 Matlab仿真结果一致，说明二维提升小波变换结构的正确。图5为α＝2时嵌入水印后的图片和算法仿真结果。由图可知，嵌入水印后对图的影响不大，基本不能被人的眼睛所感知。但当α>8时，图像质量还是有了一定的影响,这是因为LL子带包含了图像的主要信息。

本文实现了一种基于DWT域的数字水印算法，其中DWT变换算法的实现是该设计中数字水印方案的关键算法之一。采用ModelSim仿真对设计进行验证，其结果与Matlab仿真结果一致，说明了该设计的正确性。实验结果表明,该方案利用FPGA实现水印算法比用软件实现法速度更快，性能更稳定。
参考文献
[1] COX I J, MILLER M L, BLOOM J A.数字水印[M].王颖,黄志蓓,译.北京:电子工业出版社,2003.
[2] SWELDENS W. The lifting scheme: a construction of second generation wavelets [J]. SIAM J Math Anal, 1997,29(2):511-546.
[3] 乔世杰，王国裕.离散小波变换的VLSI实现[J].微电子学，2001,31(2):143-145.
[4] 张波. 基于提升小波变换的图像数字水印算法IP核的研究与设计[D]. 成都：西南交通大学，2009.
[5] 钟桦,张小华,焦李成. 数字水印与图像认证:算法及应用[M]. 西安：西安电子科技大学出版社,2006.
[6] 刘军伟. 基于FPGA的数字水印算法的设计和实现[D].成都：电子科技大学，2005.